题目内容
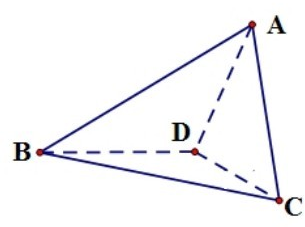 已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.
已知四面体ABCD,∠ADB=∠CDB=120°,且平面ABD⊥平面BCD.(Ⅰ)若AD=CD,求证:BD⊥AC;
(Ⅱ)求二面角B-CD-A的正切值.
考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知条件能推导出△ADB≌△CDB,从而得到AC⊥平面BDM,由此能够证明AC⊥BD.
(Ⅱ)过点A作AH⊥BD交BD延长线于H,过H作HG⊥CD于G,连结GA,由三垂线定理推导出∠AGH为二面角A-CD-H的平面角,由此能求出二面角B-CD-A的正切值.
(Ⅱ)过点A作AH⊥BD交BD延长线于H,过H作HG⊥CD于G,连结GA,由三垂线定理推导出∠AGH为二面角A-CD-H的平面角,由此能求出二面角B-CD-A的正切值.
解答:
(Ⅰ)证明:∵AD=DC,∠ADB=∠CDB=120°,BD=BD,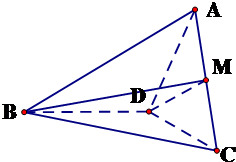
∴△ADB≌△CDB,∴AB=BC,
取AC中点M,则MB⊥AC,DM⊥AC,
∴AC⊥平面BDM,
∵BD?平面BDM,
∴AC⊥BD.(4分)
(Ⅱ)解:过点A作AH⊥BD交BD延长线于H,
过H作HG⊥CD于G,连结GA,
∵平面ABD⊥平面BCD,
∴AH⊥平面BCD,∴AH⊥CD
根据三垂线定理知,
∠AGH为二面角A-CD-H的平面角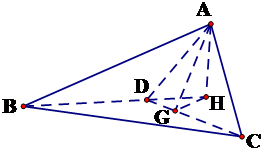 ,
,
由已知可知∠ADH=60°,
设AD=2a,则AH=
a,HD=a,
在Rt△HDG中,∵∠HDG=60°,∴HG=
a,
∴tan∠AGH=2,
∴二面角B-CD-A的正切值为-2.(10分)
注:用空间向量做,酌情给分.

∴△ADB≌△CDB,∴AB=BC,
取AC中点M,则MB⊥AC,DM⊥AC,
∴AC⊥平面BDM,
∵BD?平面BDM,
∴AC⊥BD.(4分)
(Ⅱ)解:过点A作AH⊥BD交BD延长线于H,
过H作HG⊥CD于G,连结GA,
∵平面ABD⊥平面BCD,
∴AH⊥平面BCD,∴AH⊥CD
根据三垂线定理知,
∠AGH为二面角A-CD-H的平面角
 ,
,由已知可知∠ADH=60°,
设AD=2a,则AH=
| 3 |
在Rt△HDG中,∵∠HDG=60°,∴HG=
| ||
| 2 |
∴tan∠AGH=2,
∴二面角B-CD-A的正切值为-2.(10分)
注:用空间向量做,酌情给分.
点评:本题考查异面直线垂直的证明,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.
如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.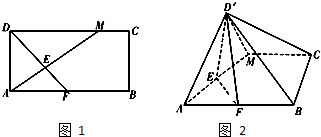 如图1,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得如图2四棱锥D′-ABCM.
如图1,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得如图2四棱锥D′-ABCM.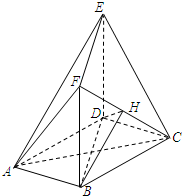 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点. 如图,AB是⊙O的一条直径,过A作⊙O的切线,在切线上取一点C,使AC=AB,连接OC,与⊙O交于点D,BD的延长线与AC交于点E,求证:
如图,AB是⊙O的一条直径,过A作⊙O的切线,在切线上取一点C,使AC=AB,连接OC,与⊙O交于点D,BD的延长线与AC交于点E,求证: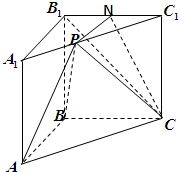 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1的运动
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1的运动