��Ŀ����
��ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+c��x�������ύ�ڵ�F��4��0������y�������ύ�ڵ�E��0��4�����߳�Ϊ4��������ABCD�Ķ���D��ԭ��O�غϣ�����A���E�غϣ�����C���F�غϣ�
��1�������ߵĺ�������ʽ��
��2����ͼ2����������ABCD��ƽ�����˶������ұ�BC���ڵ�ֱ��ʼ����x�ᴹֱ�����������AB���ڵ�P��ͬʱ���CD���ڵ�Q�����A������Ϊ��m��n��
�ٵ�PO=PFʱ���ֱ������P�͵�Q�����꼰PF����ֱ��l�ĺ�������ʽ��
�ڵ�n=2ʱ����PΪAB���е㣬�����m��ֵ��
��3������B�ڵڣ�2�����е�PF����ֱ��l���˶�����������ABCD�����������������㣬��ֱ��д��m��ȡֵ��Χ��

��1�������ߵĺ�������ʽ��
��2����ͼ2����������ABCD��ƽ�����˶������ұ�BC���ڵ�ֱ��ʼ����x�ᴹֱ�����������AB���ڵ�P��ͬʱ���CD���ڵ�Q�����A������Ϊ��m��n��
�ٵ�PO=PFʱ���ֱ������P�͵�Q�����꼰PF����ֱ��l�ĺ�������ʽ��
�ڵ�n=2ʱ����PΪAB���е㣬�����m��ֵ��
��3������B�ڵڣ�2�����е�PF����ֱ��l���˶�����������ABCD�����������������㣬��ֱ��д��m��ȡֵ��Χ��

���㣺���κ���������
ר�⣺������,���ν��,���������ʼ�Ӧ��
��������1���������߹�E��0��4����F��4��0�������������߷������ϵ��a��c���ɵ������߷��̣�
��2���ٹ���P��PG��x���ڵ�G����ͼ��P�ĺ����꣬����P��������������������ꣻ��������ABCD�ı߳���4�����Q��������Ϊ-1�����������߷�����������ꣻ
�ڵ�n=2ʱ�����P��������Ϊ2������P���������ϣ���P��2
��2����P��-2
��2�������ͼ�����mֵ��
��3����A��m��n���ɵ�CDֱ�߷�����B�����꣬�������ν��˼����⣮
��2���ٹ���P��PG��x���ڵ�G����ͼ��P�ĺ����꣬����P��������������������ꣻ��������ABCD�ı߳���4�����Q��������Ϊ-1�����������߷�����������ꣻ
�ڵ�n=2ʱ�����P��������Ϊ2������P���������ϣ���P��2
| 2 |
| 2 |
��3����A��m��n���ɵ�CDֱ�߷�����B�����꣬�������ν��˼����⣮
���
�⣺��1���������߹�E��0��4����F��4��0����
��
⇒
��
�������ߵķ���Ϊy=-
x2+4��
��2���ٹ���P��PG��x���ڵ�G����PO=PF����OG=FG��
��F��4��0������OF=4����OG=
PF=
��4=2������P�ĺ�����Ϊ2��
��P���������ϣ���y=-
��4+4=3����P��2��3����
��������ABCD�ı߳���4����Q��������Ϊ-1��
��Q���������ϣ���-1=-
x2+4⇒x=2
��-2
����ȥ����
��Q��2
��-1����
KPF=
����PF����ֱ��l�ĺ�������ʽΪy=-
��x-4����
�ڵ�n=2ʱ�����P��������Ϊ2����P���������ϣ���P��2
��2����P��-2
��2����
��PΪAB���е㣬��AP=2��
��A��2
-2��2����A��-2
-2��2������m��ֵΪ2
-2��-2
-2��
��3������B��M��ʱ��C���������ϣ�A�ĺ�������m����B�ĺ�������m+4��
����ֱ��PF�Ľ���ʽ�ã�y=-
��m+4��+6=-
m��
��B����������-
m����C�������ǣ�m+4��-
m-4����
��C��������������ߵĽ���ʽ�ã�-
m-4=-
��m+4��2+4����ã�m=-1-
��-1+
����ȥ����
��B��E��ʱ��AB���������ߵĶ��㣬��E����������4��
��y=4����y=-
x+6����4=-
x+6����ã�x=
��
��ʱA�������ǣ�-
��4����E�������ǣ���
��4������ʱ����������������3�����㣮
����B��E��ʱ�������������������������㣬��ʱ-1-
��m��-
��
����B��E��P��֮��ʱ�������������������������㣬��ʱ��-
��x��-2��
��B��P��ʱ�����������㣻
���赱B����N��ʱ��D��ͬʱ����������ʱ��
ͬ����C�������ǣ�m+4��-
m-4������D��������ǣ���m��-
m-4����
��D��������������ߵĽ���ʽ�ã�-
m-4=-
m2+4����ã�m=3+
��3-
����ȥ����
��B��F��N֮��ʱ�������������������������㣮��ʱ0��m��3+
��
��m�ķ�Χ�ǣ�-1-
��m��-
��m=2��0��m��3+
��
��
|
|
�������ߵķ���Ϊy=-
| 1 |
| 4 |
��2���ٹ���P��PG��x���ڵ�G����PO=PF����OG=FG��
��F��4��0������OF=4����OG=
| 1 |
| 2 |
| 1 |
| 2 |
��P���������ϣ���y=-
| 1 |
| 4 |
��������ABCD�ı߳���4����Q��������Ϊ-1��
��Q���������ϣ���-1=-
| 1 |
| 4 |
| 5 |
| 5 |
��Q��2
| 5 |
KPF=
| -3 |
| 2 |
| 3 |
| 2 |
�ڵ�n=2ʱ�����P��������Ϊ2����P���������ϣ���P��2
| 2 |
| 2 |
��PΪAB���е㣬��AP=2��
��A��2
| 2 |
| 2 |
| 2 |
| 2 |
��3������B��M��ʱ��C���������ϣ�A�ĺ�������m����B�ĺ�������m+4��
����ֱ��PF�Ľ���ʽ�ã�y=-
| 3 |
| 2 |
| 3 |
| 2 |
��B����������-
| 3 |
| 2 |
| 3 |
| 2 |
��C��������������ߵĽ���ʽ�ã�-
| 3 |
| 2 |
| 1 |
| 4 |
| 17 |
| 17 |
��B��E��ʱ��AB���������ߵĶ��㣬��E����������4��
��y=4����y=-
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
��ʱA�������ǣ�-
| 8 |
| 3 |
| 4 |
| 3 |
����B��E��ʱ�������������������������㣬��ʱ-1-
| 17 |
| 8 |
| 3 |
����B��E��P��֮��ʱ�������������������������㣬��ʱ��-
| 8 |
| 3 |
��B��P��ʱ�����������㣻
���赱B����N��ʱ��D��ͬʱ����������ʱ��
ͬ����C�������ǣ�m+4��-
| 3 |
| 2 |
| 3 |
| 2 |
��D��������������ߵĽ���ʽ�ã�-
| 3 |
| 2 |
| 1 |
| 4 |
| 41 |
| 41 |
��B��F��N֮��ʱ�������������������������㣮��ʱ0��m��3+
| 41 |
��m�ķ�Χ�ǣ�-1-
| 17 |
| 8 |
| 3 |
| 41 |
���������⿼���˶��κ�����ͼ�����ʣ��������������ν��˼�������⣬������ѧ��������������������

��ϰ��ϵ�д�
�����Ŀ
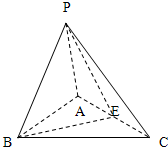 ��ͼ��������P-ABC�У�PA=PB=AB=2��AB��BC��ƽ��PAB��ƽ��ABC��EΪAC���е㣮
��ͼ��������P-ABC�У�PA=PB=AB=2��AB��BC��ƽ��PAB��ƽ��ABC��EΪAC���е㣮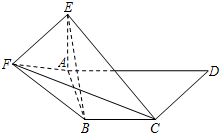 ��ͼ����ֱ������ABCD�У�AD��BC����ADC=90�㣬AE��ƽ��ABCD��EF��CD��BC=CD=AE=EF=
��ͼ����ֱ������ABCD�У�AD��BC����ADC=90�㣬AE��ƽ��ABCD��EF��CD��BC=CD=AE=EF= ��ͼ��AB��ԲO��ֱ������C��ԲO�ϲ�ͬ��A��B��һ�㣬��BAC=45�㣬��V��ԲO����ƽ����һ�㣬��VA=VB=VC��E��AC���е㣮
��ͼ��AB��ԲO��ֱ������C��ԲO�ϲ�ͬ��A��B��һ�㣬��BAC=45�㣬��V��ԲO����ƽ����һ�㣬��VA=VB=VC��E��AC���е㣮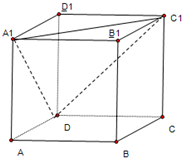 ��������ABCD-A1B1C1D1�У���ƽ��A1DC1��ƽ��ADD1A1���ɽǵ�����ֵ��
��������ABCD-A1B1C1D1�У���ƽ��A1DC1��ƽ��ADD1A1���ɽǵ�����ֵ��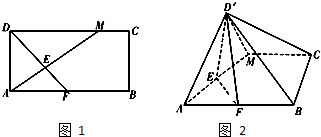 ��ͼ1���ھ���ABCD�У�AB=2BC����M�ڱ�CD�ϣ���F�ڱ�AB�ϣ���DF��AM������ΪE��������ADM��AM����ʹ��Dλ��D��λ�ã�����D��B��D��C����ͼ2����D��-ABCM��
��ͼ1���ھ���ABCD�У�AB=2BC����M�ڱ�CD�ϣ���F�ڱ�AB�ϣ���DF��AM������ΪE��������ADM��AM����ʹ��Dλ��D��λ�ã�����D��B��D��C����ͼ2����D��-ABCM��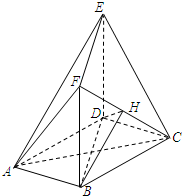 ��ͼ���ڶ�����ABCDEF�У�����ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬�ı���BDEF�Ǿ��Σ�ƽ��BDEF��ƽ��ABCD��BF=3��H��CF���е㣮
��ͼ���ڶ�����ABCDEF�У�����ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬�ı���BDEF�Ǿ��Σ�ƽ��BDEF��ƽ��ABCD��BF=3��H��CF���е㣮 ��ͼ��AB�ǡ�O��һ��ֱ������A����O�����ߣ���������ȡһ��C��ʹAC=AB������OC�����O���ڵ�D��BD���ӳ�����AC���ڵ�E����֤��
��ͼ��AB�ǡ�O��һ��ֱ������A����O�����ߣ���������ȡһ��C��ʹAC=AB������OC�����O���ڵ�D��BD���ӳ�����AC���ڵ�E����֤��