题目内容
若不等式|x|＜1成立，则不等式[x-（a+1）][x-（a+4）]＜0也成立，求实数a的取值范围．
考点：一元二次不等式的解法,函数恒成立问题
专题：不等式的解法及应用
分析：求出不等式的解集，根据不等式之间的关系建立不等式解集之间的关系，即可得到结论．
解答：
解：不等式[x-（a+1）][x-（a+4）]＜0，
则a+1＜x＜a+4，
由|x|＜1，则-1＜x＜1，
若不等式|x|＜1成立，则不等式[x-（a+1）][x-（a+4）]＜0也成立，
即{x|-1＜x＜1}⊆{x|a+1＜x＜a+4}，
即
，
∴
，
∴-3≤a≤-2，
即实数a的取值范围是[-3，-2]．
则a+1＜x＜a+4，
由|x|＜1，则-1＜x＜1，
若不等式|x|＜1成立，则不等式[x-（a+1）][x-（a+4）]＜0也成立，
即{x|-1＜x＜1}⊆{x|a+1＜x＜a+4}，
即
|
∴
|
∴-3≤a≤-2，
即实数a的取值范围是[-3，-2]．
点评：本题注意考查不等式的解法以及不等式恒成立，将不等式转化为不等式解集之间的关系是解决本题的根据．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
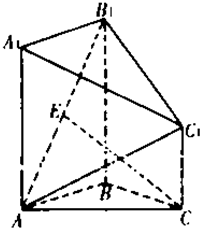如图，在几何体ABC-A1B1C1中，点A1，B1，C1在平面ABC内的正投影分别为A，B，C，且AB⊥BC，AA1=BB1=4，AB=BC=CC1=2，E为AB1中点，
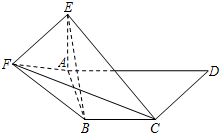如图，在直角梯形ABCD中，AD∥BC，∠ADC=90°，AE⊥平面ABCD，EF∥CD，BC=CD=AE=EF=
如图，AB是圆O的直径，点C是圆O上不同于A、B的一点，∠BAC=45°，点V是圆O所在平面外一点，且VA=VB=VC，E是AC的中点．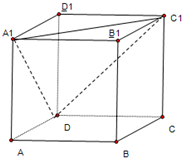
在正方体ABCD-A1B1C1D1中，求平面A1DC1与平面ADD1A1所成角的正切值．
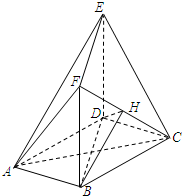如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，H是CF的中点．