题目内容
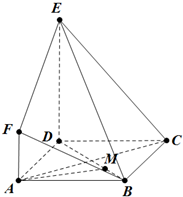 如图,ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3.
如图,ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3.(1)求证:AC⊥平面BDE;
(2)求直线AB与平面BEF所成的角的正弦值;
(3)线段BD上是否存在点M,使得AM∥平面BEF?若存在,试确定点M的位置;若不存在,说明理由.
考点:用空间向量求直线与平面的夹角,直线与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离,空间向量及应用
分析:(1)由DE⊥平面ABCD,ABCD是正方形,能够证明AC⊥平面BDE.
(2)以D为坐标原点,以DA为x轴,以DC为y轴,以DE为z轴,建立空间直角坐标系,由此能求出直线AB与平面BEF所成的角的正弦值.
(3)点M是线段BD上一个点,设M(t,t,0),由AM∥平面BEF,
•
=0,能求出点M坐标.
(2)以D为坐标原点,以DA为x轴,以DC为y轴,以DE为z轴,建立空间直角坐标系,由此能求出直线AB与平面BEF所成的角的正弦值.
(3)点M是线段BD上一个点,设M(t,t,0),由AM∥平面BEF,
| AM |
| n |
解答:
(1)证明:∵DE⊥平面ABCD,
∴DE⊥AC.…2分
∵ABCD是正方形,
∴AC⊥BD,
又BD∩DE=D
从而AC⊥平面BDE.…4分
(2)解:∵DA,DC,DE两两垂直,
∴以D为坐标原点,以DA为x轴,以DC为y轴,以DE为z轴,
建立空间直角坐标系D-xyz如图所示.
∵DE=3,由AF∥DE,DE=3AF=3
得AF=1.…6分
则A(2,0,0),F(2,0,1),E(0,0,3),B(2,2,0),∴
=(0,-2,1),
=(2,0,-2)…7分
设平面BEF的法向量为
=(x,y,z),
则
,
∴
,令z=2,则
=(2,1,2).…8分
∵
=(0,2,0)
∴直线AB与平面BEF所成的角θ满足sinθ=|cos<
,
>|=
=
=
…10分
(3)解:点M是线段BD上一个点,设M(t,t,0),
则
=(t-2,t,0),
∵AM∥平面BEF,
∴
•
=0,…11分
即2(t-2)+t=0,解得t=
.…12分
此时,点M坐标为(
,
,0).…13分.
∴DE⊥AC.…2分
∵ABCD是正方形,
∴AC⊥BD,
又BD∩DE=D
从而AC⊥平面BDE.…4分
(2)解:∵DA,DC,DE两两垂直,
∴以D为坐标原点,以DA为x轴,以DC为y轴,以DE为z轴,
建立空间直角坐标系D-xyz如图所示.

∵DE=3,由AF∥DE,DE=3AF=3
得AF=1.…6分
则A(2,0,0),F(2,0,1),E(0,0,3),B(2,2,0),∴
| BF |
| EF |
设平面BEF的法向量为
| n |
则
|
∴
|
| n |
∵
| AB |
∴直线AB与平面BEF所成的角θ满足sinθ=|cos<
| n |
| AB |
|
| ||||
|
|
| 2 |
| 2×3 |
| 1 |
| 3 |
(3)解:点M是线段BD上一个点,设M(t,t,0),
则
| AM |
∵AM∥平面BEF,
∴
| AM |
| n |
即2(t-2)+t=0,解得t=
| 4 |
| 3 |
此时,点M坐标为(
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的正弦值的求法,考查满足条件的点的坐标的求法,是中档题,解题时要注意向量法的合理运用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
下列几何体的主视图与众不同的是( )
A、 |
B、 |
C、 |
D、 |
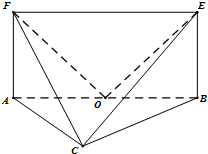 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.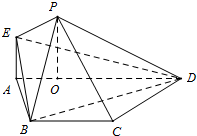 如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=
如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=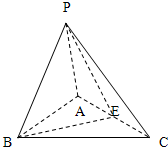 如图,在三棱锥P-ABC中,PA=PB=AB=2,AB⊥BC,平面PAB⊥平面ABC,E为AC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,AB⊥BC,平面PAB⊥平面ABC,E为AC的中点. 如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.
如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.