题目内容
15．已知f（x）是定义在R上的奇函数，且在[0，+∞）上是增函数，则f（x+1）≥0的解集为（ ）| A． | （-∞，-1] | B． | （-∞，1] | C． | [-1，+∞） | D． | [1，+∞） |
分析 根据函数奇偶性和单调性之间的关系进行转化求解即可．
解答 解：∵f（x）是定义在R上的奇函数，且在[0，+∞）上是增函数，
∴函数在（-∞，+∞）上是增函数，
∵f（0）=0，
∴不等式f（x+1）≥0等价为f（x+1）≥f（0），
则x+1≥0，得x≥-1，
即不等式的解集为[-1，+∞），
故选：C
点评 本题主要考查不等式的求解，根据函数奇偶性的性质将不等式进行转化是解决本题的关键．
练习册系列答案
相关题目
6．
如图，将无盖正方体纸盒展开，直线AB，CD在原正方体中的位置关系是（ ）
如图，将无盖正方体纸盒展开，直线AB，CD在原正方体中的位置关系是（ ）| A． | 平行 | B． | 相交成60° | C． | 相交且垂直 | D． | 异面直线 |
3．
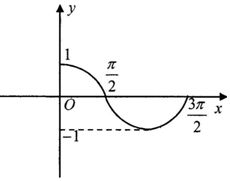已知函数f（x）=sin（ωx+φ），x∈R（其中ω＞0，-π＜φ＜π）的部分图象，如图所示．那么f（x）的解析式为（ ）
已知函数f（x）=sin（ωx+φ），x∈R（其中ω＞0，-π＜φ＜π）的部分图象，如图所示．那么f（x）的解析式为（ ）| A． | $f（x）=sin（x+\frac{π}{2}）$ | B． | $f（x）=sin（x-\frac{π}{2}）$ | C． | $f（x）=sin（2x+\frac{π}{2}）$ | D． | $f（x）=sin（2x-\frac{π}{2}）$ |
10．已知集合A={x|（x-1）（x-3）＜0}，B={x|2＜x＜4}，则A∩B=（ ）
| A． | {x|1＜x＜3} | B． | {x|1＜x＜4} | C． | {x|2＜x＜3} | D． | {x|2＜x＜4} |
20．
如图是一个组合体的三视图，根据图中数据，可得该几何体的表面积（接触面积忽略不计）是（ ）
如图是一个组合体的三视图，根据图中数据，可得该几何体的表面积（接触面积忽略不计）是（ ）| A． | 32π | B． | 36π | C． | 40π | D． | 48π |
7．已知直线l1：x-y+1=0和l2：x-y+3=0，则l1与l2之间距离是（ ）
| A． | $2\sqrt{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |