题目内容
5.已知直线2ax+by-2=0(a>0,b>0)过点(1,2),则$\frac{1}{a}+\frac{1}{b}$的最小值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
分析 根据直线过点(1,2),求出a,b的关系.利用“乘1法”与基本不等式的性质即可得出.
解答 解:直线2ax+by-2=0(a>0,b>0)过点(1,2),
可得:2a+2b=2,即a+b=1.
则$\frac{1}{a}+\frac{1}{b}$=($\frac{1}{a}+\frac{1}{b}$)(a+b)=2+$\frac{a}{b}+\frac{b}{a}$$≥2+2\sqrt{\frac{b}{a}×\frac{a}{b}}$=4.当且仅当a=b=$\frac{1}{2}$时取等号.
∴$\frac{1}{a}+\frac{1}{b}$的最小值为4.
故选C.
点评 本题考查了“乘1法”与基本不等式的性质,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20.已知数列{an}:a1=1,${a_{n+1}}=2{a_n}+3,({n∈{N^+}})$,则an=( )
| A. | 2n+1-3 | B. | 2n-1 | C. | 2n+1 | D. | 2n+2-7 |
10.已知全集U={0,1,2,3,4},集合A={1,2},B={0,2,4},则(∁UA)∩B等于( )
| A. | {0,4} | B. | {0,3,4} | C. | {0,2,3,4} | D. | {2} |
17.已知b>0,log3b=a,log6b=c,3d=6,则下列等式成立的是( )
| A. | a=2c | B. | d=ac | C. | a=cd | D. | c=ad |
15.已知f(x)是定义在R上的奇函数,且在[0,+∞)上是增函数,则f(x+1)≥0的解集为( )
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
 已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.
已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.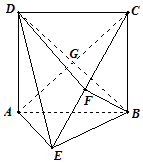 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.