题目内容
4.已知A、B是函数y=f(x),x∈[a,b]图象的两个端点,M(x,y)是f(x)上任意一点,过M(x,y)作MN⊥x轴交直线AB于N,若不等式|MN|≤k恒成立,则称函数f(x)在[a,b]上“k阶线性近似”.(1)若f(x)=x+$\frac{1}{x}$,x∈[$\frac{1}{2}$,2],证明:f(x)在[$\frac{1}{2}$,2]上“$\frac{1}{2}$阶线性近似”;
(2)若f(x)=x2在[-1,2]上“k阶线性近似”,求实数k的最小值.
分析 (1)根据对勾函数的图象和性质,得到f(x)=x+$\frac{1}{x}$,x∈[$\frac{1}{2}$,2],满足|MN|≤$\frac{1}{2}$,进而得到答案.
(2)由已知可得 N和M的横坐标相同,根据|MN|=x+2-x2=-(x-$\frac{1}{2}$)2+$\frac{9}{4}$及x∈[-1,2],求出|MN|的范围,再由|MN|≤k恒成立,求得k的取值范围.
解答 证明:(1)若f(x)=x+$\frac{1}{x}$,x∈[$\frac{1}{2}$,2],则A($\frac{1}{2}$,$\frac{5}{2}$)、B(2,$\frac{5}{2}$),
故直线AB的方程为:y=$\frac{5}{2}$,
则由|MN|=$\frac{5}{2}$-(x+$\frac{1}{x}$),
∴|MN|∈[0,$\frac{1}{2}$],
故|MN|≤$\frac{1}{2}$,
故f(x)在[$\frac{1}{2}$,2]上“$\frac{1}{2}$阶线性近似”;
解:(2)由MN⊥x交直线AB于N,得 N 和M的横坐标相同.
对于区间[-1,2]上的函数f(x)=x2 ,A(-1,1)、B(2,4),
则直线AB的方程为:y=x+2,
则有|MN|=x+2-x2=-(x-$\frac{1}{2}$)2+$\frac{9}{4}$,
∴|MN|∈[0,$\frac{9}{4}$].
再由|MN|≤k恒成立,可得 k≥$\frac{9}{4}$.
故实数k的最小值为$\frac{9}{4}$.
点评 本题考查的知识点是新定义“k阶线性近似”,正确理解新定义“k阶线性近似”,是解答的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
15.已知f(x)是定义在R上的奇函数,且在[0,+∞)上是增函数,则f(x+1)≥0的解集为( )
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
12.已知在△ABC中,∠ACB=$\frac{π}{2}$,AB=2BC,现将△ABC绕BC所在直线旋转到△PBC,设二面角P-BC-A大小为θ,PB与平面ABC所成角为α,PC与平面PAB所成角为β,若0<θ<π,则( )
| A. | $α≤\frac{π}{3}$且$sinβ≤\frac{{\sqrt{3}}}{3}$ | B. | $α≤\frac{π}{3}$且$sinβ<\frac{{\sqrt{3}}}{3}$ | C. | $α≤\frac{π}{6}$且$β≥\frac{π}{3}$ | D. | $α≤\frac{π}{6}$且$β<\frac{π}{3}$ |
9.函数y=sinx(cosx-sinx),x∈R的值域是( )
| A. | [-$\frac{1}{2}$,$\frac{3}{2}$] | B. | [$\frac{1-\sqrt{2}}{2},\frac{1+\sqrt{2}}{2}$] | C. | [-$\frac{3}{2},\frac{1}{2}$] | D. | [$\frac{-1-\sqrt{2}}{2},\frac{-1+\sqrt{2}}{2}$] |
13.设函数f(x)是定义在R上的奇函数,则下列结论中一定正确的是( )
| A. | 函数f(x)+x2是奇函数 | B. | 函数f(x)+|x|是偶函数 | ||
| C. | 函数x2f(x)是奇函数 | D. | 函数|x|f(x)是偶函数 |
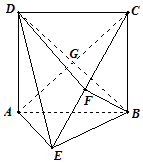 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.