题目内容
3.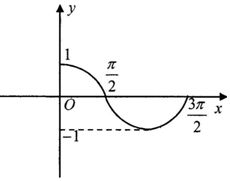 已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )
已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )| A. | $f(x)=sin(x+\frac{π}{2})$ | B. | $f(x)=sin(x-\frac{π}{2})$ | C. | $f(x)=sin(2x+\frac{π}{2})$ | D. | $f(x)=sin(2x-\frac{π}{2})$ |
分析 通过函数的图象,求出函数的周期,求出ω,利用函数经过的特殊点,求出φ,得到函数的解析式.
解答 解:由图象可知T=2($\frac{3π}{2}$-$\frac{π}{2}$)=2π,
所以可得:ω=1,
因为函数的图象经过($\frac{3π}{2}$,0),
所以0=sin($\frac{3π}{2}$+φ),由五点作图法可得:$\frac{3π}{2}$+φ=2π,
所以解得:φ=$\frac{π}{2}$,
所求函数的解析式为:y=sin(x+$\frac{π}{2}$).
故选:A.
点评 本题考查函数的图象与函数的解析式的求法,考查函数的图象的应用,考查计算能力,属于基础题.

练习册系列答案
相关题目
15.已知f(x)是定义在R上的奇函数,且在[0,+∞)上是增函数,则f(x+1)≥0的解集为( )
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
12.已知在△ABC中,∠ACB=$\frac{π}{2}$,AB=2BC,现将△ABC绕BC所在直线旋转到△PBC,设二面角P-BC-A大小为θ,PB与平面ABC所成角为α,PC与平面PAB所成角为β,若0<θ<π,则( )
| A. | $α≤\frac{π}{3}$且$sinβ≤\frac{{\sqrt{3}}}{3}$ | B. | $α≤\frac{π}{3}$且$sinβ<\frac{{\sqrt{3}}}{3}$ | C. | $α≤\frac{π}{6}$且$β≥\frac{π}{3}$ | D. | $α≤\frac{π}{6}$且$β<\frac{π}{3}$ |
13.设函数f(x)是定义在R上的奇函数,则下列结论中一定正确的是( )
| A. | 函数f(x)+x2是奇函数 | B. | 函数f(x)+|x|是偶函数 | ||
| C. | 函数x2f(x)是奇函数 | D. | 函数|x|f(x)是偶函数 |
 已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.
已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.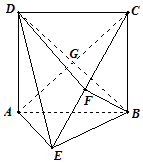 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.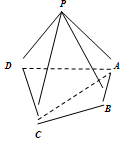 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△ADP是等腰直角三角形,∠APD是直角,AB⊥AD,AB=1,$AD=2,AC=CD=\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△ADP是等腰直角三角形,∠APD是直角,AB⊥AD,AB=1,$AD=2,AC=CD=\sqrt{5}$.