题目内容
设f(x)=kx+1,若f(2)=0,则f(3)= .
考点:函数的值
专题:函数的性质及应用
分析:利用函数的性质求解.
解答:
解:∵f(x)=kx+1,f(2)=0,
∴2k+1=0,解得k=-
,
∴f(x)=-
x+1,
∴f(3)=-
×3+1=-
.
故答案为:-
.
∴2k+1=0,解得k=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
∴f(3)=-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查函值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
在下列关于点P,直线l、m与平面α、β的命题中,正确的是( )
| A、若m⊥α,l⊥m,则l∥α |
| B、若α⊥β,α∩β=m,P∈α,P∈l,且l⊥m,则l⊥β |
| C、若l,m是异面直线,m?α,m∥β,l?β,l∥α,则α∥β |
| D、若α⊥β,且l⊥β,m⊥l,则m⊥α |
符合下列条件的三角形有且只有一个的是( )
| A、a=1,b=2,c=3 | ||
| B、a=1,b=2,∠A=100° | ||
C、a=1,b=
| ||
| D、b=c=1,∠B=45° |
数列3,7,13,21,31,…的一个通项公式是( )
| A、an=4n-1 |
| B、an=n2+n+1 |
| C、an=2+2n-n2 |
| D、an=n(n2-1) |
函数f(x)=2-x的大致图象为( )
A、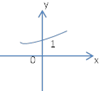 |
B、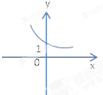 |
C、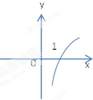 |
D、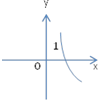 |
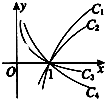 已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为
已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为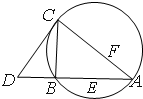 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.