题目内容
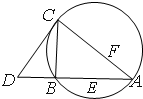 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.(Ⅰ)证明:CA是△ABC外接圆的直径;
(Ⅱ)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值.
考点:与圆有关的比例线段
专题:立体几何
分析:(I)由已知与圆的切线的性质可得△CDB∽△AEF,∠DBC=∠EFA.利用B,E,F,C四点共圆,可得∠CFE=∠DBC,∠EFA=∠CFE=90°,即可证明.
(II)连接CE,由于∠CBE=90°,可得过B,E,F,C四点的圆的直径为CE,由DB=BE,有CE=DC,又BC2DB•BA=2DB2,可得CA2=4DB2+BC2=6DB2,而DC2=DB•DA=3DB2,即可得出.
(II)连接CE,由于∠CBE=90°,可得过B,E,F,C四点的圆的直径为CE,由DB=BE,有CE=DC,又BC2DB•BA=2DB2,可得CA2=4DB2+BC2=6DB2,而DC2=DB•DA=3DB2,即可得出.
解答:
(I)证明:∵CD为△ABC外接圆的切线,
∴∠BCB=∠A,由题设知:
=
,
故△CDB∽△AEF,∴∠DBC=∠EFA.
∵B,E,F,C四点共圆,
∴∠CFE=∠DBC,故∠EFA=∠CFE=90°
∴∠CBA=90°,因此CA是△ABC外接圆的直径.
(2)解:连接CE,
∵∠CBE=90°,
∴过B,E,F,C四点的圆的直径为CE,
由DB=BE,有CE=DC,
又BC2DB•BA=2DB2,∴CA2=4DB2+BC2=6DB2,
而DC2=DB•DA=3DB2,
故B,E,F,C四点的圆的面积与△ABC的外接圆面积的比值为
.

∴∠BCB=∠A,由题设知:
| BC |
| FA |
| DC |
| EA |
故△CDB∽△AEF,∴∠DBC=∠EFA.
∵B,E,F,C四点共圆,
∴∠CFE=∠DBC,故∠EFA=∠CFE=90°
∴∠CBA=90°,因此CA是△ABC外接圆的直径.
(2)解:连接CE,
∵∠CBE=90°,
∴过B,E,F,C四点的圆的直径为CE,
由DB=BE,有CE=DC,
又BC2DB•BA=2DB2,∴CA2=4DB2+BC2=6DB2,
而DC2=DB•DA=3DB2,
故B,E,F,C四点的圆的面积与△ABC的外接圆面积的比值为
| 1 |
| 2 |
点评:本题考查了圆的切线的性质、四点共圆的性质、勾股定理、圆的面积与三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
将直线l:x-y+1=0绕着点A(2,3)逆时针方向旋转90°,得到直线l1的方程是( )
| A、x-2y+4=0 |
| B、x+y-1=0 |
| C、x+y-5=0 |
| D、2x+y-7=0 |
函数f(x)=x3-ax+1在区间[2,+∞)内是增函数,则实数a的取值范围是( )
| A、a≤12 | B、a<12 |
| C、a≥12 | D、a>12 |
圆心为(1,-1),半径为2的圆的方程是( )
| A、(x-1)2+(y+1)2=2 |
| B、(x-1)2+(y-1)2=4 |
| C、(x+1)2+(y-1)2=2 |
| D、(x-1)2+(y+1)2=4 |
若α∈(-
,
],则cosα的范围是( )
| π |
| 6 |
| π |
| 3 |
A、(-
| ||||||
B、(-
| ||||||
C、[
| ||||||
D、[
|
两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为( )
| A、-1 | B、2 | C、0 | D、3 |