Question

已知椭圆C的中心在坐标原点，焦点在x轴上，C的短轴长为4，离心率为

3

2

．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过原点且与坐标轴不垂直的直线交椭圆C于P₁，P₂两点，B₁，B₂分别是椭圆C的上、下顶点，B₁P₂与x轴交于Q点，直线P₁B₁与直线QB₂相交于点P，求P点的轨迹方程．

Answer 1

考点：轨迹方程,椭圆的标准方程,直线与圆锥曲线的关系

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）设出椭圆方程，利用已知结合隐含条件求得长半轴长，则椭圆方程可求；
（Ⅱ）设出直线P₁P₂的方程，和椭圆方程联立求得P₁，P₂的坐标，写出B₁P₂的方程，得到Q点的坐标，然后得到P₁B₁的方程和QB₂的方程，联立后求解交点，消掉参数k后得答案．

解答： 解：（Ⅰ）设椭圆方程为：

x2

a2

+

y2

b2

=1(a＞b＞0)，
2b=4，b=2，

c

a

=

3

2

，
∴

c2

a2

=

3

4

，即

a2-b2

a2

=

3

4

，解得a²=16．
∴椭圆C的方程为

x2

16

+

y2

4

=1；
（Ⅱ）如图，

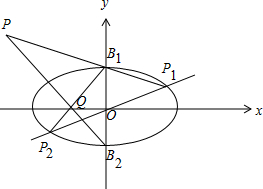
设P（x，y），直线P₁P₂为y=kx（k≠0），
联立

y=kx x2 16 + y2 4 =1

，得P1(

4

1+4k2

，

4k

1+4k2

)，P2(-

4

1+4k2

，-

4k

1+4k2

)，
则B₁P₂的方程为

y+ 4k 1+4k2

2+ 4k 1+4k2

=

x+ 4 1+4k2

4 1+4k2

，
取y=0，得Q（-

4

2k+ 1+4k2

，0），
则P₁B₁的方程为：

y-2

4k 1+4k2 -2

=

x-0

4 1+4k2 -0

  ①，
QB₂的方程为：

y-0

-2-0

=

x+ 4 2k+ 1+4k2

4 2k+ 1+4k2

  ②，
联立①②可得：

x=- 2 k y= 1+4k2 k

．
消去参数k得：x²-4y²+16=0（x≠0）．

点评：本题考查了椭圆方程的求法，考查了直线和圆锥曲线的位置关系，训练了利用参数法求曲线的方程，考查了学生的计算能力，是压轴题．