题目内容
直线y=x+1交x轴于点P,交椭圆
-
=1于相异两点A、B,且
=-3
.
(1)求a的取值范围;
(2)将弦AB绕点A逆时针旋转90°得到线段AQ,设点Q坐标为(m,n),求证:m+7n=-1.
| x2 |
| a2 |
| y2 |
| b2 |
| PA |
| PB |
(1)求a的取值范围;
(2)将弦AB绕点A逆时针旋转90°得到线段AQ,设点Q坐标为(m,n),求证:m+7n=-1.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由y=x+1,
+
=1联立,得(a2+b2)y2-2b2y+b2-a2b2=0,设A(y1-1,y1),B(y2-1,y2),由根的判别式和韦达定理能求出a的取值范围.
(2)由题疫知
=(4y2,4y2),
=(-4y2,4y2),由此推导出m=-7y2-1,n=y2,从而能够证明m+7n=-1.
| x2 |
| a2 |
| y2 |
| b2 |
(2)由题疫知
| AB |
| AQ |
解答:
解:(1)由y=x+1,得x=y-1,
代入
+
=1,得(a2+b2)y2-2b2y+b2-a2b2=0,
设A(y1-1,y1),B(y2-1,y2),则y1,y2是这个一元二次方程的根,
△=(-2b2)2-4(a2+b2)(b2-a2b2)>0,
∴a2+b2>1,①
由
=-
,P(-1,0)得y1=-3y2,
y1+y2=-2y2=
,②
y1y2=-3y2=
,③
由②式得y2=-
,代入③式,得-
=
,
∴b2=
,④
由a>b,及①④,得
,
解不等式组,得1<a2<
,
又∵a>0,
∴a的取值范围是(1,
).
(2)证明:
=(y2-y1,y2-y1)=(4y2,4y2),
依题意
=(-4y2,4y2),
∵
=
+
,
∴(m-n)=(y1-1,y1)+(-4y2,4y2)
=(-3y2-1,-3y2)+(-4y2,4y2)=(-7y2-1,y2),
∴m=-7y2-1,n=y2,
∴m+7n=-1.
代入
| x2 |
| a2 |
| y2 |
| b2 |
设A(y1-1,y1),B(y2-1,y2),则y1,y2是这个一元二次方程的根,
△=(-2b2)2-4(a2+b2)(b2-a2b2)>0,
∴a2+b2>1,①
由
| PA |
| PB |
y1+y2=-2y2=
| 2b2 |
| a2+b2 |
y1y2=-3y2=
| b2-a2b2 |
| a2+b2 |
由②式得y2=-
| b2 |
| a2+b2 |
| 3b4 |
| (a2+b2) |
| b2-a2b2 |
| a2+b2 |
∴b2=
| a2(a2-1) |
| 4-a2 |
由a>b,及①④,得
|
解不等式组,得1<a2<
| 5 |
| 2 |
又∵a>0,
∴a的取值范围是(1,
| ||
| 2 |
(2)证明:
| AB |
依题意
| AQ |
∵
| OQ |
| OA |
| AQ |
∴(m-n)=(y1-1,y1)+(-4y2,4y2)
=(-3y2-1,-3y2)+(-4y2,4y2)=(-7y2-1,y2),
∴m=-7y2-1,n=y2,
∴m+7n=-1.
点评:本题考查a的取值范围的求法,考查等式的证明,解题时要注意平面向量的运算,合理地运用函数与方程思想、等价转化思想.

练习册系列答案
相关题目
下列命题中真命题是( )
| A、命题“存在x∈R,x2-x-2≥0”的否定是:“不存在x∈R,x2-x-2<0” | ||||||||||
B、线性回归直线
| ||||||||||
C、存在x∈(0,
| ||||||||||
D、函数f(x)=x
|
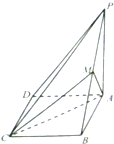 如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=
如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=