题目内容
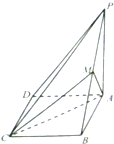 如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=
如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=| 1 |
| 2 |
(1)求证:PD∥平面AMC;
(2)求锐二面角B-AC-M的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(1)连接BD,设BD与AC相交于点O,连接OM,由已知条件知OM为△PBD的中位线,由此能证明PD∥平面ANC.
?(2)设AB=BC=2,由已知条件推导出
=
,从而得到PA⊥AB,且PA=2
,取AB的中点F,连接MF,作FG⊥AC,垂足为G,连接MG,由已知条件推导出∠MGF为二面角B-AC-M的平面角,由此能求出二面角B-AC-M的余弦值.
?(2)设AB=BC=2,由已知条件推导出
| 2 |
| sin30° |
| 4 |
| sin∠PAB |
| 3 |
解答:
 (本小题满分14分)
(本小题满分14分)
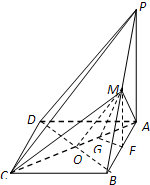
解:(1)证明:连接BD,设BD与AC相交于点O,连接OM,
∵?四边形ABCD是平行四边形,∴点O为BD的中点.…(2分)
∵M为PB的中点,∴OM为△PBD的中位线,
∴OM∥PD.?????????…(4分)
∵OM?平面AMC,PD不包含于平面AMC,
∴PD∥平面ANC.…(6分)
?(2)不妨设AB=BC=2,则PB=4.
在△PAB中,
=
,
得sin∠PAB=1,∴∠PAB=90°,
即PA⊥AB,且PA=2
.…(8分)
∵BC⊥平面PAB,PA?平面PAB,
∴PA⊥BC,
∵BC∩AB=B,∴PA⊥平面ABCD.
取AB的中点F,连接MF,则MF∥PA,
且MF=
PA=
.…(10分)???
∴MF⊥平面ABCD.AC?平面ABCD,∴MF⊥AC.
作FG⊥AC,垂足为G,连接MG,MF∩FG=F,
∴AC⊥平面MGF,∴AC⊥MG.
∴∠MGF为二面角B-AC-M的平面角.?…(12分)
在Rt△AFG中,∠BAC=45°,得GF=
.
在Rt△MGF中,cos∠MGF=
=
=
.
∴二面角B-AC-M的余弦值为
.…(14分)
 (本小题满分14分)
(本小题满分14分)解:(1)证明:连接BD,设BD与AC相交于点O,连接OM,
∵?四边形ABCD是平行四边形,∴点O为BD的中点.…(2分)
∵M为PB的中点,∴OM为△PBD的中位线,
∴OM∥PD.?????????…(4分)
∵OM?平面AMC,PD不包含于平面AMC,
∴PD∥平面ANC.…(6分)
?(2)不妨设AB=BC=2,则PB=4.
在△PAB中,
| 2 |
| sin30° |
| 4 |
| sin∠PAB |
得sin∠PAB=1,∴∠PAB=90°,
即PA⊥AB,且PA=2
| 3 |
∵BC⊥平面PAB,PA?平面PAB,
∴PA⊥BC,
∵BC∩AB=B,∴PA⊥平面ABCD.
取AB的中点F,连接MF,则MF∥PA,
且MF=
| 1 |
| 2 |
| 3 |
∴MF⊥平面ABCD.AC?平面ABCD,∴MF⊥AC.
作FG⊥AC,垂足为G,连接MG,MF∩FG=F,
∴AC⊥平面MGF,∴AC⊥MG.
∴∠MGF为二面角B-AC-M的平面角.?…(12分)
在Rt△AFG中,∠BAC=45°,得GF=
| ||
| 2 |
在Rt△MGF中,cos∠MGF=
| GF |
| MG |
| ||||
|
| ||
| 7 |
∴二面角B-AC-M的余弦值为
| ||
| 7 |
点评:本题考查直线与平面平行的证明,考查二面角和余弦值的求法,解题时要注意正弦定理的合理运用.

练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn,已知(a5-1)3+2009(a5-1)=1,(a2005-1)3+2009(a2005-1)=-1,则下列结论中正确的是( )
| A、S2009=2009,a2005<a5 |
| B、S2009=2009,a2005>a5 |
| C、S2009=-2009,a2005≤a5 |
| D、S2009=-2009,a2005≥a5 |
如图所示的算法流程图中,最后一个输出的数是( )


A、
| ||
| B、2 | ||
C、
| ||
| D、3 |