题目内容
在数列{an}中,a1=3,a17=67,通项公式是关于n的一次函数.
(1)求数列{an}的通项公式;
(2)求a2011;
(3)2011是否为数列{an}中的项?若是,为第几项?
(1)求数列{an}的通项公式;
(2)求a2011;
(3)2011是否为数列{an}中的项?若是,为第几项?
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:(1)设an=kn+b(k≠0),由已知得
,从而能求出an=4n-1.
(2)由an=4n-1,能求出a2011.
(3)令2011=4n-1,能求出2011是数列{an}的第503项.
|
(2)由an=4n-1,能求出a2011.
(3)令2011=4n-1,能求出2011是数列{an}的第503项.
解答:
解:(1)设an=kn+b(k≠0),
∵a1=3,a17=67,
∴
,
解得k=4,b=-1.
∴an=4n-1.
(2)∵an=4n-1,
∴a2011=4×2011-1=8043.
(3)令2011=4n-1,解得n=503∈N*,
∴2011是数列{an}的第503项.
∵a1=3,a17=67,
∴
|
解得k=4,b=-1.
∴an=4n-1.
(2)∵an=4n-1,
∴a2011=4×2011-1=8043.
(3)令2011=4n-1,解得n=503∈N*,
∴2011是数列{an}的第503项.
点评:本题考查等差数列的性质的应用,是基础题,解题时要认真审题.

练习册系列答案
相关题目
一植物园参观路径如图所示,若要全部参观并且路线不重复,则不同的参观路线种数共有( )
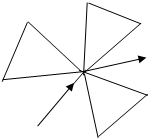

| A、6种 | B、8种 |
| C、36种 | D、48种 |
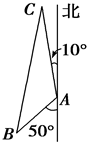 我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.
我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.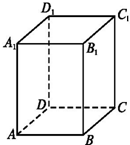 如图,已知长方体ABCD-A1B1C1D1中,AB=
如图,已知长方体ABCD-A1B1C1D1中,AB=