题目内容
3.在空间中,a、b、c是三条不同的直线,α、β是两个不同的平面,则下列为真命题的是( )| A. | 若a∥α,a∥b,b∥c,则c∥α | B. | 若a?α,b?β,α⊥β,则a⊥b | ||
| C. | 若a⊥α,a⊥b,b⊥c,则c⊥α | D. | 若α∥β,a?α,则a∥β |
分析 A,由a∥b,b∥c,可得c∥a,有可能c?α,即可判断出正误;
B,分别位于两个相互垂直的平面内的两条直线还可能是平行的或异面的,即可判断出正误;
C,由a⊥b,b⊥c并不能推出a∥c,虽然a⊥α,也不能推出c⊥α,即可判断出正误;
D,利于面面平行的性质定理、线面平行的判定定理即可判断出正误.
解答 解:对于A,由a∥b,b∥c,可得c∥a,但若两个平行直线中的一条平行于一个平面,则另一条不一定平行于该平面,有可能在该平面内,因此选项A不正确;
对于B,分别位于两个相互垂直的平面内的两条直线还可能是平行的或异面的,因此选项B不正确;
对于C,由a⊥b,b⊥c并不能推出a∥c,故结合a⊥α也不能推出c⊥α,除非a,b,c是同一平面内的三条直线才成立,故此时结论不正确.即选项C不正确;
对于D,直线a与平面β没有公共点,因此,选项D正确.
故选:D.
点评 本题考查了空间线面位置关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.函数$y=\frac{{\sqrt{x}}}{x-1}$的定义域为( )
| A. | [0,1)∪(1,+∞) | B. | (0,+∞) | C. | (0,1) | D. | [0,1] |
8.若“?x∈R,x2+mx+2m-3≥0”为假命题,则m的取值范围是( )
| A. | (-∞,2]∪[6,+∞) | B. | (-∞,2)∪(6,+∞) | C. | [2,6] | D. | (2,6) |
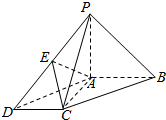 在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点. 如图,直三陵柱ABC-A1B1C1中,△ABC为等腰直角三角形,AC=BC=1,AA1=$\sqrt{2}$,D是A1B1的中点,F是B1B上一点.
如图,直三陵柱ABC-A1B1C1中,△ABC为等腰直角三角形,AC=BC=1,AA1=$\sqrt{2}$,D是A1B1的中点,F是B1B上一点.