题目内容
已知A是B的必要条件,B是C的充分条件,则A是C的( )
| A、充分条件 | B、必要条件 |
| C、充要条件 | D、无法判断 |
考点:必要条件、充分条件与充要条件的判断
专题:常规题型,推理和证明
分析:将题意转化为推出的形式,从而确定选项.
解答:
解:∵A是B的必要条件,
∴B⇒A,
∵B是C的充分条件,
∴B⇒C.
故无法判断A是C的条件,
故选 D.
∴B⇒A,
∵B是C的充分条件,
∴B⇒C.
故无法判断A是C的条件,
故选 D.
点评:本题考查了充分条件与必要条件,属于基础题.

练习册系列答案
相关题目
已知cosα=-
,则sin(30°+α)+sin(30°-α)的值为( )
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知函数f(x)=ex-e-x-sinx,若a,b∈R,则a+b>0是f(a)+f(b)>0成立的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
自然数都是整数,而-2是整数,所以-2是自然数.以上三段论推理错在( )
| A、大前提不正确 |
| B、小前提不正确 |
| C、省略了大前提 |
| D、推理形式不正确 |
若X~B(n,p)(x服从以n,p为参数的二项分布),且E(X)=6,D(X)=3,则P(X=1)=( )
| A、3•2-2 |
| B、2-4 |
| C、3•2-10 |
| D、2-8 |
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)>0的解集是( )
| A、(-3,0)∪(0,3) |
| B、(-3,0)∪(3,+∞) |
| C、(-∞,-3)∪(3,+∞) |
| D、(-∞,-3)∪(0,3) |
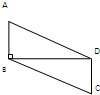 如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则空间四边形ABCD的对角线AC的长度为
如图,在平行四边形ABCD中,2|AB|2+|BD|2-4=0,∠ABD=90°,沿BD折成直二面角A-BD-C,则空间四边形ABCD的对角线AC的长度为