题目内容
记函数f(x)的定义域为D,若f(x)满足:
(1)?x1,x2∈D,当x1≠x2时,
>0;
(2)?x∈D,f(x+2)-f(x+1)≥f(x+1)-f(x),则称函数f(x)具有性质P.
现有以下四个函数:
①f(x)=x2,x∈(0,+∞);②f(x)=ex;③f(x)=lnx;④f(x)=cosx
则具有性质P的为 (把所有符合条件的函数编号都填上).
(1)?x1,x2∈D,当x1≠x2时,
| f(x1)-f(x2) |
| x1-x2 |
(2)?x∈D,f(x+2)-f(x+1)≥f(x+1)-f(x),则称函数f(x)具有性质P.
现有以下四个函数:
①f(x)=x2,x∈(0,+∞);②f(x)=ex;③f(x)=lnx;④f(x)=cosx
则具有性质P的为
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:依题意,在同一直角坐标系中,分别作出①f(x)=x2,x∈(0,+∞);②f(x)=ex;③f(x)=lnx;④f(x)=cosx的图象,即可得到答案.
解答:
解:由(1)知函数f(x)为定义域D上的增函数;
由(2)知,f(x+2)+f(x)≥2f(x+1),即
≥f(x+1);
在同一直角坐标系中,分别作出①f(x)=x2,x∈(0,+∞);②f(x)=ex;③f(x)=lnx;④f(x)=cosx的图象,

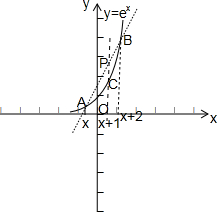
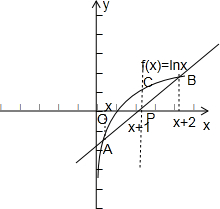
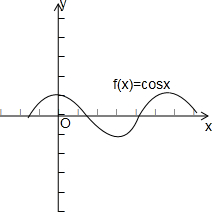
由图可知,具有性质P的为①②.
故答案为:①②.
由(2)知,f(x+2)+f(x)≥2f(x+1),即
| f(x+2)+f(x) |
| 2 |
在同一直角坐标系中,分别作出①f(x)=x2,x∈(0,+∞);②f(x)=ex;③f(x)=lnx;④f(x)=cosx的图象,

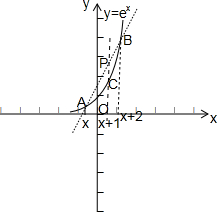


由图可知,具有性质P的为①②.
故答案为:①②.
点评:本题考查命题的真假判断与应用,着重考查基本初等函数的单调性与凸性,作图是关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的焦距为2
,过M(1,1)斜率为
直线l交曲线C于A,B且M是线段AB的中点,则双曲线C的标准方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=2|X-1|的图象为( )
A、 |
B、 |
C、 |
D、 |
已知集合M={5,6,7},N={5,7,8},则( )
| A、M⊆N |
| B、M?N |
| C、M∩N={5,7} |
| D、M∪N={6,7,8} |
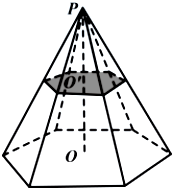 如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′. 如图所示,在水平放置的边长为40cm的正方形轨道模型上,质点甲从A点出发以8cm/s的速度沿点A-B-C方向运动,同时另一质点乙从B点出发以10cm/s的速度沿点B-C-D方向运动.
如图所示,在水平放置的边长为40cm的正方形轨道模型上,质点甲从A点出发以8cm/s的速度沿点A-B-C方向运动,同时另一质点乙从B点出发以10cm/s的速度沿点B-C-D方向运动.