题目内容
已知函数f（x）是偶函数，g（x）是奇函数，且满足2f（x）+g（x）=（x-1）2，求f（x）和g（x）的解析式．
考点：函数奇偶性的性质,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：直接利用函数的奇偶性，列出方程，通过解方程即可求出f（x）和g（x）的解析式．
解答：
解：根据题意，
∵f（x）是偶函数，g（x）是奇函数，
且f（x）+g（x）=（x-1）2①，
∴f（-x）=f（x），g（-x）=-g（x），
∴f（-x）+g（-x）=（-x-1）2，
即f（x）-g（x）=（x+1）2②；
由①+②解得f（x）=x2+1，
①-②解得g（x）=-2x．
∵f（x）是偶函数，g（x）是奇函数，
且f（x）+g（x）=（x-1）2①，
∴f（-x）=f（x），g（-x）=-g（x），
∴f（-x）+g（-x）=（-x-1）2，
即f（x）-g（x）=（x+1）2②；
由①+②解得f（x）=x2+1，
①-②解得g（x）=-2x．
点评：本题考查了函数的奇偶性的应用问题，解题时应根据题意，结合奇偶性建立二元一次方程组，从而求出答案来，是基础题．
练习册系列答案
相关题目
已知三角形△ABC的三边长构成公差为2的等差数列，且最大角的正弦值为
，则这个三角形的周长为（ ）
| ||
| 2 |
| A、15 | B、18 | C、21 | D、24 |
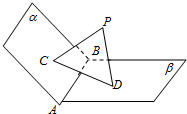如图，已知平面α，β，且α∩β=AB，PC⊥α，PD⊥β，C，D是垂足．且PC=PD=CD=1，则二面角α-AB-β的大小是（ ）| A、120° | B、45° |
| C、60° | D、150° |