题目内容
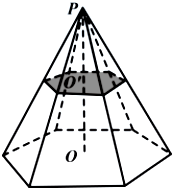 如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.(1)求大棱锥、小棱锥、棱台的侧面面积之比;
(2)若大棱锥PO的侧棱长为12cm,小棱锥的底面边长为4cm,求截得的棱台的侧面面积和表面积.
考点:棱柱、棱锥、棱台的体积,棱柱、棱锥、棱台的侧面积和表面积
专题:综合题,空间位置关系与距离
分析:(1)设小棱锥的底面边长为a,斜高为h,则大棱锥的底面边长为2a,斜高为2h,计算出大棱锥、小棱锥、棱台的侧面面积,可得结论;
(2)先计算大棱锥的侧面面积,再求截得的棱台的侧面面积和表面积.
(2)先计算大棱锥的侧面面积,再求截得的棱台的侧面面积和表面积.
解答:
解:(1)设小棱锥的底面边长为a,斜高为h,则大棱锥的底面边长为2a,斜高为2h,
∴大棱锥的侧面面积为6×
×2a×2h=12ah,小棱锥的侧面面积为6×
ah=3ah,
∴棱台的侧面面积为9ah,
∴大棱锥、小棱锥、棱台的侧面面积之比为4:1:3;
(2)∵小棱锥的底面边长为4cm,
∴大棱锥的底面边长为8cm,
∵大棱锥PO的侧棱长为12cm,
∴斜高为
=8
,
∴大棱锥的侧面面积为
×8×8
=32
,
∴棱台的侧面面积为24
,
棱台的上底面积为6×
×42=24
,下底面积为6×
×82=96
,
∴截得的棱台的表面积为120
+32
cm2.
∴大棱锥的侧面面积为6×
| 1 |
| 2 |
| 1 |
| 2 |
∴棱台的侧面面积为9ah,
∴大棱锥、小棱锥、棱台的侧面面积之比为4:1:3;
(2)∵小棱锥的底面边长为4cm,
∴大棱锥的底面边长为8cm,
∵大棱锥PO的侧棱长为12cm,
∴斜高为
| 144-16 |
| 2 |
∴大棱锥的侧面面积为
| 1 |
| 2 |
| 2 |
| 2 |
∴棱台的侧面面积为24
| 2 |
棱台的上底面积为6×
| ||
| 4 |
| 3 |
| ||
| 4 |
| 3 |
∴截得的棱台的表面积为120
| 3 |
| 2 |
点评:本题考查棱柱、棱锥、棱台的侧面积和表面积,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
