题目内容

已知双曲线与椭圆
x2
16
+
y2
4
=1焦点相同，且其一条渐近线方程为x-
2
y=0，求该双曲线方程．
考点：双曲线的标准方程
专题：圆锥曲线的定义、性质与方程
分析：由已知，可设双曲线方程为x2-2y2=λ，由于双曲线与椭圆
x2
16
+
y2
4
=1焦点相同，可确定λ的值，从而求出双曲线方程．
解答： 解：∵双曲线的渐近线方程为x-
2
y=0，
∴可设双曲线方程为
x2-2y2=λ，
由于双曲线与椭圆
x2
16
+
y2
4
=1焦点相同，
∴λ＞0．
将x2-2y2=λ化为标准方程，得
x2
λ
-
y2
λ
2
=1，
则有λ+
λ
2
=16-4=12，
解得λ=8，
故双曲线方程为
x2
8
-
y2
4
=1．
点评：本题考查椭圆方程，双曲线简单几何性质的应用．属于中档题．解题的关键是渐近线的应用．
练习册系列答案
相关题目
已知向量
a
=（
3
，-1），
b
=（
1
2
，
3
2
），
（1）求证：
a
⊥
b
；
（2）若存在不同时为0的实数k和t，使
x
=
a
+（t-3）
b
，
y
=-k
a
+t
b
，且
x
⊥
y
，试求函数关系式k=f（t）；
（3）求函数k=f（t）的最小值．
四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD．E为SD的中点，已知∠ABC=45°，AB=2，BC=2
2
，SB=SC=
3
．
（Ⅰ） 求证：SA⊥BC；
（Ⅱ） 在BC上求一点F，使EC∥平面SAF；
（Ⅲ） 求三棱锥D-EAC的体积．
已知椭圆
8x2
81
+
y2
36
=1上一点M的纵坐标为2．
（1）求M的横坐标；
（2）求过M且与
x2
9
+
y2
4
=1共焦点的椭圆的方程．
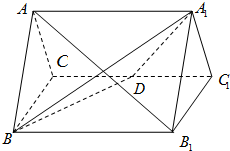如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1的中点．
（1）求证：AB1⊥平面A1BD；
（2）求二面角A-A1D-B的正弦值；
（3）求点C到平面A1BD的距离．
若 0＜α＜
π
2
，-
π
2
＜β＜0，cos（α+
π
4
）=
1
3
，cos（
π
4
-
β
2
）=
3
3
，求cos（2α+β）值．
已知平面直角坐标系内三点A、B、C在一条直线上，
OA
=（-2，m），
OB
=（n，1），
OC
=（5，-1），且
OA
⊥
OB
，其中O为坐标原点．
（1）求实数m，n的值；
（2）设△OAC的重心为G，若存在实数λ，使
OB
=λ
OG
，试求∠AOC的大小．
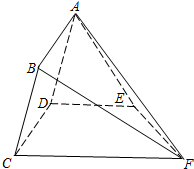如图，矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角，DE∥CF，CD⊥DE，AD=2，EF=3
2
，CF=6，∠CFE=45°．
（Ⅰ）求证：BF∥平面ADE；
（Ⅱ）在线段CF上求一点G，使锐二面角B-EG-D的余弦值为
1
4
．
设P（x0，y0）是椭圆
x2
16
+
y2
9
=1上一动点，F1，F2是椭圆的两个焦点，则
|PF1|
•
|PF2|
的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网