题目内容
已知向量
=（
，-1），
=（
，
），
（1）求证：
⊥
；
（2）若存在不同时为0的实数k和t，使
=
+（t-3）
，
=-k
+t
，且
⊥
，试求函数关系式k=f（t）；
（3）求函数k=f（t）的最小值．
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
（1）求证：
| a |
| b |
（2）若存在不同时为0的实数k和t，使
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
（3）求函数k=f（t）的最小值．
考点：平面向量数量积的运算,平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：（1）根据向量
和
的坐标，利用两个向量的数量积公式求得
•
=0，可得
⊥
．
（2）根据|
|=2，|
|=1，
•
=0，
⊥
，求得
•
=[
+(t-3)
]•（k
+t
）=0，可得函数关系式k=f（t）．
（3）由（2）可得k=
=
，利用二次函数的性质求得它的最小值．
| a |
| b |
| a |
| b |
| a |
| b |
（2）根据|
| a |
| b |
| a |
| b |
| x |
| y |
| x |
| y |
| a |
| b |
| a |
| b |
（3）由（2）可得k=
| t2-3t |
| 4 |
(t-
| ||||
| 4 |
解答：
解：（1）∵向量
=（
，-1），
=（
，
），∴
•
=
×
+（-1）×
=0，
∴
⊥
．
（2）∵|
|=2，|
|=1，
•
=0，
⊥
，
∴
•
=[
+(t-3)
]•（-k
+t
）=-k
2+（-kt+3k+t）
•
+t（t-3）
2
=-k×4+0+t（t-3）×1=0，
∴k=
(t≠0，t≠3)．
（3）根据 k=
=
，∴当t=
时，kmin=-
．
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴
| a |
| b |
（2）∵|
| a |
| b |
| a |
| b |
| x |
| y |
∴
| x |
| y |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
=-k×4+0+t（t-3）×1=0，
∴k=
| t2-3t |
| 4 |
（3）根据 k=
| t2-3t |
| 4 |
(t-
| ||||
| 4 |
| 3 |
| 2 |
| 9 |
| 16 |
点评：本题主要考查两个向量坐标形式的运算，两个向量垂直的性质，两个向量的数量积公式，属于中档题．
练习册系列答案
应用题作业本系列答案
相关题目
若不等式ax2+bx+c≥0的解集是{x|-1≤x≤2}，则不等式cx2+bx+a＜0的解集是（ ）
A、（-∞，-1）∪（
| ||
B、（-
| ||
C、（-∞，-
| ||
D、（-1，
|
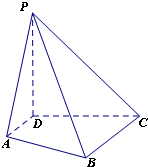在四棱锥P-ABCD中，PD⊥平面ABCD，PD=CD=BC=2AD，AD∥BC，∠BCD=90°．
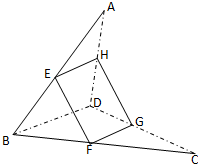如图，已知四边形ABCD是空间四边形，E是AB的中点，F，G分别是BC，CD上的点，且