题目内容
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.E为SD的中点,已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.E为SD的中点,已知∠ABC=45°,AB=2,BC=2| 2 |
| 3 |
(Ⅰ) 求证:SA⊥BC;
(Ⅱ) 在BC上求一点F,使EC∥平面SAF;
(Ⅲ) 求三棱锥D-EAC的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)首先根据直线与平面垂直的判定定理证明BC⊥平面SAG,再利用线面垂直的性质即可证明BC⊥SA.
(Ⅱ)根据已知条件可猜测点F的位置,证明即可.利用直线与平面平行的判定定理可以证明当点F为BC中点时,EC∥平面SAF.
(Ⅲ)根据平面与平面垂直的性质定理得到SG⊥平面ABCD.从而得到点E到平面ABCD的距离.再利用等积法即可求出三棱锥D-EAC的体积.
(Ⅱ)根据已知条件可猜测点F的位置,证明即可.利用直线与平面平行的判定定理可以证明当点F为BC中点时,EC∥平面SAF.
(Ⅲ)根据平面与平面垂直的性质定理得到SG⊥平面ABCD.从而得到点E到平面ABCD的距离.再利用等积法即可求出三棱锥D-EAC的体积.
解答:
证明:(Ⅰ)连接AC
∵∠ABC=45°,AB=2,BC=
.
在△ABC中,由余弦定理可得,AC=2.
∴AC=AB.取BC的中点G,连接SG,AG.
则AG⊥BC.
∵SB=SC
∴SG⊥BC
又∵AG∩SG=G.
∴BC⊥平面SAG.
∵SA?平面SAG,
∴BC⊥SA.
(Ⅱ)当F为BC中点时,EC∥平面SAF.
取SA的中点M,连接EM,MF.
∵E为SD中点,
∴EM∥DA且EM=
DA.
又∵CF∥DA且CF=
DA,
∴EM∥CF且EM=CF.
∴四边形EMFC为平行四边形.
∴EC∥MF.
∵MG?平面SAF,EC?平面SAF,
∴EC∥平面SAF.
(Ⅲ)∵平面SBC⊥平面ABCD,
SG?平面SBC,
平面SBC∩平面ABCD=BC,
SG⊥BC,
∴SG⊥平面ABCD.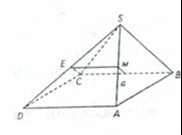
在△SBC中,
BC=2
,SB=SC=
.
∴SG=1.
∵E为SD的中点,
∴点E到平面ABCD的距离为
.
∴VD-EAC=VE-DAC=
•
•2•2•
=
.
∵∠ABC=45°,AB=2,BC=
| 2 |
在△ABC中,由余弦定理可得,AC=2.
∴AC=AB.取BC的中点G,连接SG,AG.
则AG⊥BC.
∵SB=SC
∴SG⊥BC
又∵AG∩SG=G.
∴BC⊥平面SAG.
∵SA?平面SAG,
∴BC⊥SA.
(Ⅱ)当F为BC中点时,EC∥平面SAF.
取SA的中点M,连接EM,MF.
∵E为SD中点,
∴EM∥DA且EM=
| 1 |
| 2 |
又∵CF∥DA且CF=
| 1 |
| 2 |
∴EM∥CF且EM=CF.
∴四边形EMFC为平行四边形.
∴EC∥MF.
∵MG?平面SAF,EC?平面SAF,
∴EC∥平面SAF.
(Ⅲ)∵平面SBC⊥平面ABCD,
SG?平面SBC,
平面SBC∩平面ABCD=BC,
SG⊥BC,
∴SG⊥平面ABCD.

在△SBC中,
BC=2
| 2 |
| 3 |
∴SG=1.
∵E为SD的中点,
∴点E到平面ABCD的距离为
| 1 |
| 2 |
∴VD-EAC=VE-DAC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查直线与平面平行,垂直的判定定理,平面与平面垂直的性质定理.以及用等积法求三棱锥的体积等知识.属于中档题.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
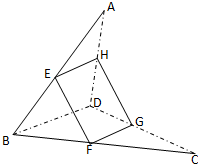 如图,已知四边形ABCD是空间四边形,E是AB的中点,F,G分别是BC,CD上的点,且
如图,已知四边形ABCD是空间四边形,E是AB的中点,F,G分别是BC,CD上的点,且