题目内容
已知椭圆
+
=1上一点M的纵坐标为2．
（1）求M的横坐标；
（2）求过M且与
+
=1共焦点的椭圆的方程．
| 8x2 |
| 81 |
| y2 |
| 36 |
（1）求M的横坐标；
（2）求过M且与
| x2 |
| 9 |
| y2 |
| 4 |
考点：椭圆的简单性质,双曲线的标准方程
专题：圆锥曲线的定义、性质与方程
分析：（1）将点M的纵坐标代入方程即可解得横坐标．
（2）利用椭圆方程得出焦点坐标，利用椭圆定义得出a2，即可求出椭圆方程．
（2）利用椭圆方程得出焦点坐标，利用椭圆定义得出a2，即可求出椭圆方程．
解答：
解：（1）把M的纵坐标2代入椭圆方程
+
=1，
得
+
=1．
解得，x=±3．
∴M的横坐标为3或-3．
（2）∵
+
=1，
∴焦点坐标为F1（-
，0），F2(
，0)．
由椭圆定义知，
|MF1|+|MF2|=2a．
即2a=
+
．
∴4a2=60．
∴a2=15．
∴b2=a2-c2=10．
故所求椭圆的方程为
+
=1．
| 8x2 |
| 81 |
| y2 |
| 36 |
得
| 8x2 |
| 81 |
| 4 |
| 36 |
解得，x=±3．
∴M的横坐标为3或-3．
（2）∵
| x2 |
| 9 |
| y2 |
| 4 |
∴焦点坐标为F1（-
| 5 |
| 5 |
由椭圆定义知，
|MF1|+|MF2|=2a．
即2a=
(3-
|
(3+
|
∴4a2=60．
∴a2=15．
∴b2=a2-c2=10．
故所求椭圆的方程为
| x2 |
| 15 |
| y2 |
| 10 |
点评：本题考查椭圆的方程的应用，椭圆的定义以及基本运算能力．属于中档题．
练习册系列答案
相关题目
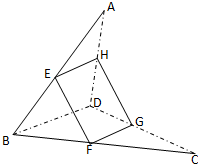如图，已知四边形ABCD是空间四边形，E是AB的中点，F，G分别是BC，CD上的点，且
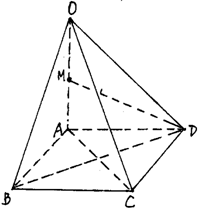如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA中点．
如图，在平行六面体ABCD-A1B1C1D1中，E，H分别是AA1、BB1的中点，求证：