题目内容
已知平面直角坐标系内三点A、B、C在一条直线上,
=(-2,m),
=(n,1),
=(5,-1),且
⊥
,其中O为坐标原点.
(1)求实数m,n的值;
(2)设△OAC的重心为G,若存在实数λ,使
=λ
,试求∠AOC的大小.
| OA |
| OB |
| OC |
| OA |
| OB |
(1)求实数m,n的值;
(2)设△OAC的重心为G,若存在实数λ,使
| OB |
| OG |
考点:数量积判断两个平面向量的垂直关系,平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:(1)由已知向量的坐标求出
,
的坐标,由
∥
列关于m,n的方程组,再由
⊥
得到关于m,n的另一方程组,联立后求得m,n的值;
(2)由△OAC的重心为G,结合
=λ
可知B为AC的中点,由中点坐标结合(1)中的结果得到m,n的值,得到
,
的坐标,然后代入平面向量的数量积公式求得∠AOC的大小.
| AC |
| AB |
| AC |
| AB |
| OA |
| OB |
(2)由△OAC的重心为G,结合
| OB |
| OG |
| OA |
| OC |
解答:
解:(1)由于A、B、C三点在一条直线上,则
∥
,
而
=
-
=(7,-1-m),
=
-
=(n+2,1-m),
∴7(1-m)-(-1-m)(n+2)=0,即9-5m+mn+n=0,
又
⊥
,∴-2n+m=0,
联立方程组
,解得
或
;
(2)若存在实数λ,使
=λ
,则B为AC的中点,故m=3,n=
.
∴
=(-2,3),
=(5,-1).
∴cos∠AOC=
=
=-
,
∴∠AOC=
.
| AC |
| AB |
而
| AC |
| OC |
| OA |
| AB |
| OB |
| OA |
∴7(1-m)-(-1-m)(n+2)=0,即9-5m+mn+n=0,
又
| OA |
| OB |
联立方程组
|
|
|
(2)若存在实数λ,使
| OB |
| OG |
| 3 |
| 2 |
∴
| OA |
| OC |
∴cos∠AOC=
| ||||
|
|
| -13 | ||||
|
| ||
| 2 |
∴∠AOC=
| 3π |
| 4 |
点评:本题考查了向量共线和向量垂直的坐标运算,考查了利用数量积公式求向量的夹角,解答此题的关键是由△OAC的重心为G,且
=λ
得到B为AC的中点,是中档题.
| OB |
| OG |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=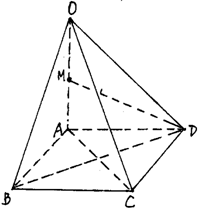 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.