题目内容
二次函数f(x)=x2+mx+1图象的对称轴是x=1,
(1)求m的值;
(2)当x∈[0,4]时,求函数的值域.
(1)求m的值;
(2)当x∈[0,4]时,求函数的值域.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由对称轴是x=-
=1,解出即可;(2)由(1)得:f(x)=x2-2x+1=(x-1)2,从而求出函数的单调区间,进而求出函数的最值,从而得出函数的值域.
| m |
| 2 |
解答:
解:(1)∵对称轴是x=-
=1,解得:m=-2,
(2)由(1)得:f(x)=x2-2x+1=(x-1)2,
∴f(x)在[0,1)递减,在(1,4]递增,
∴f(x)min=f(1)=0,f(x)max=f(4)=9,
∴函数f(x)的值域是:[0,9].
| m |
| 2 |
(2)由(1)得:f(x)=x2-2x+1=(x-1)2,
∴f(x)在[0,1)递减,在(1,4]递增,
∴f(x)min=f(1)=0,f(x)max=f(4)=9,
∴函数f(x)的值域是:[0,9].
点评:本题考查了二次函数的性质,考查了函数的单调性,函数的最值问题,是一道基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
己知函数f(x)=lnx-
,则函数f(x)的零点所在的区间是( )
| x |
| 4 |
| A、.(0,1) |
| B、(1,2) |
| C、.(2,3) |
| D、(3,4) |
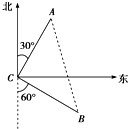 两灯塔A、B与海洋观察站C的距离都等于2
两灯塔A、B与海洋观察站C的距离都等于2| 2 |
| A、2 km |
| B、3 km |
| C、4 km |
| D、5 km |
若变量x,y满足约束条件
则Z=2x-y的最大值为( )
|
| A、2 | B、5 | C、1 | D、4 |