题目内容
已知数列{an}、{bn}满足a1=2,an-1=an(an+1-1),bn=an-1,数列{bn}的前n项和为Sn,n∈N*.
(1)证明数列{
}为等差数列,并求数列{bn}的通项公式;
(2)用数学归纳法证明:对任意的n∈N*,有1+
≤S2n≤
+n成立.
(1)证明数列{
| 1 |
| bn |
(2)用数学归纳法证明:对任意的n∈N*,有1+
| n |
| 2 |
| 1 |
| 2 |
考点:数学归纳法,等差关系的确定,数列递推式
专题:选作题,不等式
分析:(1)由bn-bn+1=bnbn+1,确定
-
=1,可得数列{
}是首项为1,公差为1的等差数列,即可求数列{bn}的通项公式;
(2)由数学归纳法的步骤,我们先判断n=1时,不等式成立;然后假设当n=k时,不等式成立,即1+
≤S2k≤
+k,证明当n=k+1时,不等式成立.
| 1 |
| bn+1 |
| 1 |
| bn |
| 1 |
| bn |
(2)由数学归纳法的步骤,我们先判断n=1时,不等式成立;然后假设当n=k时,不等式成立,即1+
| k |
| 2 |
| 1 |
| 2 |
解答:
证明:(1)由bn=an-1得an=bn+1代入an-1=an(an+1-1)得bn=(bn+1)bn+1
整理得bn-bn+1=bnbn+1,
∵bn≠0否则an=1,与a1=2矛盾
从而得
-
=1,
∵b1=a1-1=1,
∴数列{
}是首项为1,公差为1的等差数列,
∴
=n,即bn=
.
(2)用数学归纳法证明:
①当n=1时1+
=1+
,S2n=1+
,
+n=
+1,不等式成立;
②假设当n=k(k≥1,k∈N*)时,不等式成立,即1+
≤S2k≤
+k,那么当n=k+1时S2k+1=1+
+…+
+…+
≥1+
+
+…+
>1+
+
=1+
+
=1+
-S2k+1=1+
+…+
+…+
≤
+k+
+…+
<
+k+
=
+(k+1)
∴当n=k+1时,不等式成立
由①②知对任意的n∈N*,不等式成立.
整理得bn-bn+1=bnbn+1,
∵bn≠0否则an=1,与a1=2矛盾
从而得
| 1 |
| bn+1 |
| 1 |
| bn |
∵b1=a1-1=1,
∴数列{
| 1 |
| bn |
∴
| 1 |
| bn |
| 1 |
| n |
(2)用数学归纳法证明:
①当n=1时1+
| n |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②假设当n=k(k≥1,k∈N*)时,不等式成立,即1+
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| k |
| 2 |
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
| k |
| 2 |
| ||||||
| 2k个 |
| k |
| 2 |
| 1 |
| 2 |
| k+1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2 |
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
| 1 |
| 2 |
| ||||||
| 2k个 |
=
| 1 |
| 2 |
∴当n=k+1时,不等式成立
由①②知对任意的n∈N*,不等式成立.
点评:数学归纳法的步骤:①证明n=1时A式成立②然后假设当n=k时,A式成立③证明当n=k+1时,A式也成立④下绪论:A式对所有的正整数n都成立.

练习册系列答案
相关题目
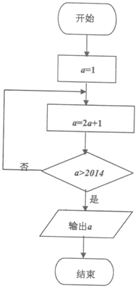 根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….
根据如图所示的程序框图,变量a每次赋值后的结果依次记作:a1、a2、a3…an….如a1=1,a2=3….