题目内容
已知函数f(x)=-
x3+
x2-2x,g(x)=
x3-
x2+(a+2)x+
-lnx,(a∈R)
(Ⅰ)当a=3时,x∈[
,2],求函数f(x)的最大值;
(Ⅱ)当a≥-1时,讨论函数F(x)=f(x)+g(x)的单调性;
(Ⅲ)若过点(0,-
)可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
| 1 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
| a |
| 2 |
| a+1 |
| x |
(Ⅰ)当a=3时,x∈[
| 3 |
| 2 |
(Ⅱ)当a≥-1时,讨论函数F(x)=f(x)+g(x)的单调性;
(Ⅲ)若过点(0,-
| 1 |
| 3 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(Ⅰ)当a=3时,x∈[
,2],求导数,确定函数的单调性,即可求函数f(x)的最大值;
(Ⅱ)当a≥-1时,分类讨论,利用导数的正负,即可得出函数F(x)=f(x)+g(x)的单调性;
(Ⅲ)先求出切线方程,点(0,-
)代入,化简可得
t3-
t2+
=0.过点(0,-
)可作函数y=f(x)图象的三条不同切线,等价于
t3-
t2+
=0有三个不同的实数解,g(t)=
t3-
t2+
,则函数的极大值与极小值异号,即可得出结论.
| 3 |
| 2 |
(Ⅱ)当a≥-1时,分类讨论,利用导数的正负,即可得出函数F(x)=f(x)+g(x)的单调性;
(Ⅲ)先求出切线方程,点(0,-
| 1 |
| 3 |
| 2 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
解答:
解:(Ⅰ)当a=3时,f′(x)=-x2+3x-2=-(x-1)(x-2),
∴x∈[
,2]时,f′(x)>0,函数单调递增,
∴函数f(x)的最大值为f(2)=-
;
(Ⅱ)F(x)=f(x)+g(x)=ax+
-lnx,F′(x)=
.
a=0,F′(x)=-
,∵x>0,∴F′(x)<0,函数在(0,+∞)上单调递减;
a>0,F′(x)=
>0,x>
,∴函数在(0,
)上单调递减;在(
,+∞)上单调
递增;
-1≤a<0,F′(x)=
<0,函数在(0,+∞)上单调递减;
(Ⅲ)设切点为P(t,-
t3+
t2-2t),则切线斜率为k=f′(t)=-t2+at-2,
∴切线方程为y+
t3-
t2+2t=(-t2+at-2)(x-t),
点(0,-
)代入,化简可得
t3-
t2+
=0.
∵过点(0,-
)可作函数y=f(x)图象的三条不同切线,
∴
t3-
t2+
=0有三个不同的实数解.
令g(t)=
t3-
t2+
,则函数的极大值与极小值异号,
由g′(t)=2t2-at=0,可得t=0或t=
,
∴
(
•
-
•
+
)<0,
∴a>2.
∴x∈[
| 3 |
| 2 |
∴函数f(x)的最大值为f(2)=-
| 2 |
| 3 |
(Ⅱ)F(x)=f(x)+g(x)=ax+
| a+1 |
| x |
| ax2-x-(a+1) |
| x2 |
a=0,F′(x)=-
| x+1 |
| x2 |
a>0,F′(x)=
| (x+1)(ax-a-1) |
| x2 |
| a+1 |
| a |
| a+1 |
| a |
| a+1 |
| a |
递增;
-1≤a<0,F′(x)=
| (x+1)(ax-a-1) |
| x2 |
(Ⅲ)设切点为P(t,-
| 1 |
| 3 |
| a |
| 2 |
∴切线方程为y+
| 1 |
| 3 |
| a |
| 2 |
点(0,-
| 1 |
| 3 |
| 2 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
∵过点(0,-
| 1 |
| 3 |
∴
| 2 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
令g(t)=
| 2 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
由g′(t)=2t2-at=0,可得t=0或t=
| a |
| 2 |
∴
| 1 |
| 3 |
| 2 |
| 3 |
| a3 |
| 8 |
| a |
| 2 |
| a2 |
| 4 |
| 1 |
| 3 |
∴a>2.
点评:本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性与极值,考查分类讨论,等价转化的数学思想,有难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
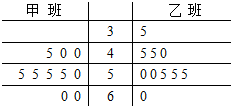 某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示:
某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示: