题目内容
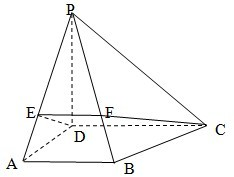 已知四棱锥P-ABCD,PD⊥面ABCD,AB∥DC,AD⊥DC,AD=
已知四棱锥P-ABCD,PD⊥面ABCD,AB∥DC,AD⊥DC,AD=| 2 |
(Ⅰ)求证:EF∥AB;
(Ⅱ)求证:AP⊥面EFCD;
(Ⅲ)求PC与面EFCD所成角的正弦值.
考点:直线与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(Ⅰ)由AB∥DC,DC?面PAB,AB?面PAB,根据线面平行的判定定理推断出DC∥面PAB,又面PAB∩面DEFC=EF根据线面平行的性质可推断出EF∥DC,进而可知EF∥AB.
(Ⅱ)由PD⊥面ABCD,推断出PD⊥CD,又AD⊥CD,PD∩AD=D线面垂直的判定定理知CD⊥面PAD,进而可知AP⊥CD,又AP⊥ED,CD∩DE=D,推断出AP⊥面EFCD,
(Ⅲ)以D为原点,DA,DC,DP分别为x,y,z轴建立空间直角坐标系,则P,C,A,
,
分别可知,设E(x,0,z)由
⊥
且
∥
可得
,解得x和z,进而求得E点坐标,设
=(m,n,p)为平面EFCD的一个法向量则有
,令m=1,p=-
,则
可求得,最后利用向量是数量积求得PC与面EFCD所成角的余弦值,则其正弦值可得..
(Ⅱ)由PD⊥面ABCD,推断出PD⊥CD,又AD⊥CD,PD∩AD=D线面垂直的判定定理知CD⊥面PAD,进而可知AP⊥CD,又AP⊥ED,CD∩DE=D,推断出AP⊥面EFCD,
(Ⅲ)以D为原点,DA,DC,DP分别为x,y,z轴建立空间直角坐标系,则P,C,A,
| AP |
| PC |
| DE |
| AP |
| AP |
| AE |
|
| n |
|
| 2 |
| n |
解答:
解:(Ⅰ)AB∥DC,DC?面PAB,AB?面PAB,
∴DC∥面PAB,
又∵面PAB∩面DEFC=EF
∴EF∥DC,
∴EF∥AB.
(Ⅱ)∵PD⊥面ABCD,
∴PD⊥CD,
又AD⊥CD,PD∩AD=D
∴CD⊥面PAD,
∵AP?面PAD,
∴AP⊥CD,
又∵AP⊥ED,CD∩DE=D
∴AP⊥面EFCD,
(Ⅲ)以D为原点,DA,DC,DP分别为x,y,z轴建立空间直角坐标系,
P(0,0,2),C(0,4,0),A(
,0,0),
=(-
,0,2),
=(0,4,-2),
设E(x,0,z)由
⊥
且
∥
可得
,解得
,∴E(
,0,
),
设
=(m,n,p)为平面EFCD的一个法向量则有
,令m=1,p=-
,∴
=(1,0,-
),
cos<
,
>=
=
∴PC与面EFCD所成角的正弦值为
.
∴DC∥面PAB,
又∵面PAB∩面DEFC=EF
∴EF∥DC,
∴EF∥AB.
(Ⅱ)∵PD⊥面ABCD,
∴PD⊥CD,
又AD⊥CD,PD∩AD=D
∴CD⊥面PAD,
∵AP?面PAD,
∴AP⊥CD,
又∵AP⊥ED,CD∩DE=D
∴AP⊥面EFCD,
(Ⅲ)以D为原点,DA,DC,DP分别为x,y,z轴建立空间直角坐标系,
P(0,0,2),C(0,4,0),A(
| 2 |
| AP |
| 2 |
| PC |
设E(x,0,z)由
| DE |
| AP |
| AP |
| AE |
|
|
2
| ||
| 3 |
| 2 |
| 3 |
设
| n |
|
| 2 |
| n |
| 2 |
cos<
| n |
| PC |
2
| ||||
|
| ||
| 15 |
∴PC与面EFCD所成角的正弦值为
| ||
| 15 |
点评:本题主要考查了线面平行,线面垂直的判定定理和性质,空间法向量的运用.考查了学生基础知识的综合运用.

练习册系列答案
相关题目