题目内容
已知函数f（x）=2
sinxcosx+2cos2x-1
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求f（x）在区间[-
，
]上的最大值和最小值．
| 3 |
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求f（x）在区间[-
| π |
| 6 |
| π |
| 4 |
考点：两角和与差的正弦函数,三角函数的周期性及其求法,正弦函数的定义域和值域
专题：常规题型,三角函数的图像与性质
分析：（Ⅰ）先逆用二倍角公式，然后逆用两角和的正弦公式化成正弦型函数的标准形式，利用周期公式T=
求周期；
（Ⅱ）根据正弦函数的最值结合定义域求函数y=2sin（2x+
）最值．
| 2π |
| |ω| |
（Ⅱ）根据正弦函数的最值结合定义域求函数y=2sin（2x+
| π |
| 6 |
解答：
解：（Ⅰ）∵f（x）=2
sinxcosx+2cos2x-1
=
sin2x+cos2x
=2sin（2x+
）
∴T=
=π．
（Ⅱ）∵x∈[-
，
]，∴2x+
∈[-
，
]
∴-1≤2sin（2x+
）≤2
∴函数f（x）在区间[-
，
]上的最小值为-1，最大值为2．
| 3 |
=
| 3 |
=2sin（2x+
| π |
| 6 |
∴T=
| 2π |
| 2 |
（Ⅱ）∵x∈[-
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
∴-1≤2sin（2x+
| π |
| 6 |
∴函数f（x）在区间[-
| π |
| 6 |
| π |
| 4 |
点评：本题考查了三角变换及三角函数的图象与性质，解题的关键是化成正弦型函数的标准形式．
练习册系列答案
相关题目
如图四边形ABEF是等腰梯形，AB∥EF，AF=BE=2，EF=4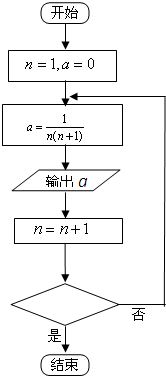
执行如图程序框图：
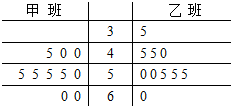某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩（满分60分），统计后获得成绩数据的茎叶图（以十位数字为茎，个位数字为叶），如图所示：