题目内容
判断并证明:函数f(x)=
在(-1,﹢∞)上的单调性.
| 2x+3 |
| x+1 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据分式函数的性质,判断函数的单调性,然后根据函数单调性的定义进行证明即可.
解答:
解:f(x)=
=
=2+
,在(-1,﹢∞)上的单调递减.
任意设-1<x1<x2,
则f(x1)-f(x2)=
-
=
,
∵-1<x1<x2,
∴x2-x1>0,
则f(x1)-f(x2)>0,
∴f(x1)>f(x2),
即函数f(x)=
在(-1,﹢∞)上的单调递减.
| 2x+3 |
| x+1 |
| 2(x+1)+1 |
| x+1 |
| 1 |
| x+1 |
任意设-1<x1<x2,
则f(x1)-f(x2)=
| 1 |
| x1+1 |
| 1 |
| x2+1 |
| x2-x1 |
| (x1+1)(x2+1) |
∵-1<x1<x2,
∴x2-x1>0,
则f(x1)-f(x2)>0,
∴f(x1)>f(x2),
即函数f(x)=
| 2x+3 |
| x+1 |
点评:本题主要考查函数单调性的判断和证明,利用函数单调性的定义是解决本题的关键.

练习册系列答案
相关题目
如图,在边长为2的正方形内有一内切圆,现从正方形内取一点P,则点P在圆内的概率为( )


A、
| ||
B、
| ||
C、
| ||
| D、π |
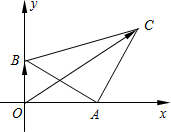 如图,等腰Rt△ABC直角边的两端点A,B分别在x轴、y轴的正半轴上移动,若|AB|=2,则
如图,等腰Rt△ABC直角边的两端点A,B分别在x轴、y轴的正半轴上移动,若|AB|=2,则