题目内容
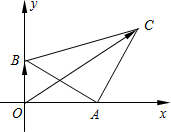如图，等腰Rt△ABC直角边的两端点A，B分别在x轴、y轴的正半轴上移动，若|AB|=2，则| OB |
| OC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设∠OAB=θ．可得OB=ABsinθ=2sinθ，＜
，
＞=
+θ，BC=2
．利用
•
=
•(
+
)=
2+
•
即可得出．
| OB |
| BC |
| π |
| 4 |
| 2 |
| OB |
| OC |
| OB |
| OB |
| BC |
| OB |
| OB |
| BC |
解答：
解：设∠OAB=θ．
则OB=ABsinθ=2sinθ，＜
，
＞=
+θ，BC=2
．
∴
•
=
•(
+
)
=
2+
•
=(2sinθ)2+2sinθ•2
•cos(
+θ)
=4sin2θ+4sinθ（cosθ-sinθ）
=2sin2θ≤2．
当θ=
时，取等号．
因此
•
的最大值是2．
故答案为：2．
则OB=ABsinθ=2sinθ，＜
| OB |
| BC |
| π |
| 4 |
| 2 |
∴
| OB |
| OC |
| OB |
| OB |
| BC |
=
| OB |
| OB |
| BC |
=(2sinθ)2+2sinθ•2
| 2 |
| π |
| 4 |
=4sin2θ+4sinθ（cosθ-sinθ）
=2sin2θ≤2．
当θ=
| π |
| 4 |
因此
| OB |
| OC |
故答案为：2．
点评：本题考查了利用数量积、三角函数的单调性、两角和差的余弦公式、倍角公式等基础知识与基本技能方法，属于基础题．
练习册系列答案
相关题目
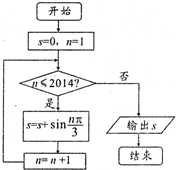
若某程序框图如图所示，则该程序运行后输出的值是（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|