题目内容
已知x>0,y>0,且lg2x+lg8y=lg4,求z=
+
的最小值.
| 1 |
| x |
| 1 |
| y |
考点:基本不等式在最值问题中的应用,对数的运算性质,基本不等式
专题:不等式的解法及应用
分析:利用对数运算法则求出x+3y=2,然后利用基本不等式求解z的最小值即可.
解答:
解:由lg2x+lg8y=lg4可得xlg2+3ylg2=2lg2∴x+3y=2
则z=
+
=
(x+3y)(
+
)=
(4+
+
)≥
(4+2
)=2+
“=”在
=
即x=
-1,y=1-
时成立.
z=
+
的最小值:2+
.
则z=
| 1 |
| x |
| 1 |
| y |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| 2 |
| x |
| y |
| 3y |
| x |
| 1 |
| 2 |
| 3 |
| 3 |
“=”在
| x |
| y |
| 3y |
| x |
| 3 |
| ||
| 3 |
z=
| 1 |
| x |
| 1 |
| y |
| 3 |
点评:本题考查基本不等式的应用,对数的运算法则,考查计算能力.

练习册系列答案
相关题目
在圆的方程x2+y2+Dx+Ey+F=0中,若D2=E2>4F,则( )
| A、圆与两坐标轴都相切 |
| B、圆与两坐标轴都相交 |
| C、圆与两坐标轴都相离 |
| D、圆心到两坐标轴的距离相等 |
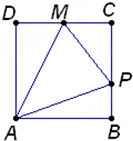 如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )
如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )A、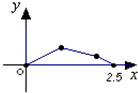 |
B、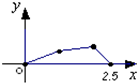 |
C、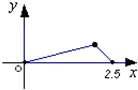 |
D、 |
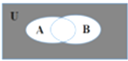 已知U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},则Venn图中阴影部分所表示的集合为( )
已知U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},则Venn图中阴影部分所表示的集合为( )| A、{3} |
| B、{4,5,6,7,8} |
| C、{7,8} |
| D、{1,2,7,8} |
 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若