题目内容
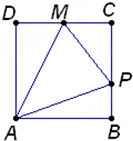 如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )
如图,点P在边长为1的正方形ABCD的边界上运动,设M是CD边的中点,当点P沿着A,B,C,M匀速率运动时,点P经过的路程x为自变量,三角形APM的面积为y,则函数y=f(x)图象的形状大致是( )A、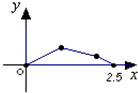 |
B、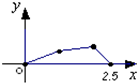 |
C、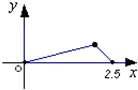 |
D、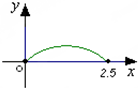 |
考点:函数的图象
专题:函数的性质及应用
分析:分:当点在AB上移动时、当点在BC上移动时、当点在CD上时,讨论y随x的变化关系.
解答:
解:根据题意和图形可知:点P按A⇒B⇒C⇒M的顺序在边长为1的正方形边上运动,△APM的面积分为3段;
当点在AB上移动时,高不变底边逐渐变大,故面积逐渐变大;
当点在BC上移动时,如图:设正方形的边长为1,
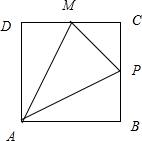
则y=S正方形-S△ADM-S△ABP-S△PCM
=1-
-
×1×(x-1)-
×
×(2-x)=-
x+
,此函数是关于x的递减函数;
当点在CD上时,高不变,底边变小故面积越来越小直到0为止.
故选:A.
当点在AB上移动时,高不变底边逐渐变大,故面积逐渐变大;
当点在BC上移动时,如图:设正方形的边长为1,

则y=S正方形-S△ADM-S△ABP-S△PCM
=1-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
当点在CD上时,高不变,底边变小故面积越来越小直到0为止.
故选:A.
点评:要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.

练习册系列答案
相关题目