题目内容
某箱装有30个零件,其中5件次品,现从中任意取出4件,用X表示取到次品的件数,列出X的分布列,并求出:
(1)所取出的4件零件中没有次品的概率;
(2)所取出的4件零件中恰有2件次品的概率;
(3)所取出的4件零件中至多有2件次品的概率.
(1)所取出的4件零件中没有次品的概率;
(2)所取出的4件零件中恰有2件次品的概率;
(3)所取出的4件零件中至多有2件次品的概率.
考点:离散型随机变量及其分布列
专题:应用题,概率与统计
分析:X是取出的次品件数,取值可以是0,1,2,3,4,利用古典概型的概率公式,即可求得结论.
解答:
解:X是取出的次品件数,取值可以是0,1,2,3,4,
则P(X=0)=
,P(X=1)=
,P(X=2)=
,P(X=3)=
,P(X=4)=
(1)所取出的4件零件中没有次品的概率P(X=0)=
=0.4616;
(2)所取出的4件零件中恰有2件次品的概率P(X=2)=
=0.1095;
(3)所取出的4件零件中至多有2件次品的概率=P(X=0)+P(X=1)+P(X=2)=0.9707.
则P(X=0)=
| ||
|
| ||||
|
| ||||
|
| ||||
|
| ||
|
(1)所取出的4件零件中没有次品的概率P(X=0)=
| ||
|
(2)所取出的4件零件中恰有2件次品的概率P(X=2)=
| ||||
|
(3)所取出的4件零件中至多有2件次品的概率=P(X=0)+P(X=1)+P(X=2)=0.9707.
点评:本题考查离散型随机变量及其分布列,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
在复平面内,复数z=1-i对应于点P,则该点在以原点为极点,实轴的正半轴为极轴的极坐标系中所对应的极坐标是( )
A、(
| ||||
B、(2,
| ||||
C、(
| ||||
D、(2,
|
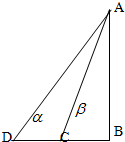 如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于
如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于