题目内容
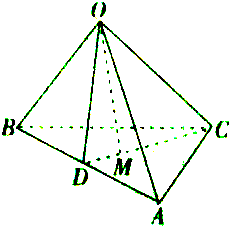如图所示，点D是AB的中点，点M是△ABC三条中线的交点，O是空间任意一点．求证：（1）
| OD |
| 1 |
| 2 |
| OA |
| OB |
（2）
| OM |
| 1 |
| 3 |
| OA |
| OB |
| OC |
考点：空间向量的加减法
专题：空间向量及应用
分析：（1）点D是AB的中点，利用平行四边形法则可得
+
=2
，即可证明；
（2）由于点M是△ABC三条中线的交点，可得
=
，
=
(
+
)=
(
-
+
-
)，
因此
=
+
=
+
(
+
-2
)即可得出．
| OA |
| OB |
| OD |
（2）由于点M是△ABC三条中线的交点，可得
| CM |
| 2 |
| 3 |
| CD |
| CD |
| 1 |
| 2 |
| CB |
| CA |
| 1 |
| 2 |
| OB |
| OC |
| OA |
| OC |
因此
| OM |
| OC |
| CM |
| OC |
| 1 |
| 3 |
| OA |
| OB |
| OC |
解答：
证明：（1）∵点D是AB的中点，∴
+
=2
，∴
=
（
+
）；
（2）∵点M是△ABC三条中线的交点，∴
=
，
=
(
+
)=
(
-
+
-
)=
(
+
-2
)，
∴
=
(
+
-2
)．
∴
=
+
=
+
(
+
-2
)=
(
+
+
)．
| OA |
| OB |
| OD |
| OD |
| 1 |
| 2 |
| OA |
| OB |
（2）∵点M是△ABC三条中线的交点，∴
| CM |
| 2 |
| 3 |
| CD |
| CD |
| 1 |
| 2 |
| CB |
| CA |
| 1 |
| 2 |
| OB |
| OC |
| OA |
| OC |
| 1 |
| 2 |
| OB |
| OA |
| OC |
∴
| CM |
| 1 |
| 3 |
| OA |
| OB |
| OC |
∴
| OM |
| OC |
| CM |
| OC |
| 1 |
| 3 |
| OA |
| OB |
| OC |
| 1 |
| 3 |
| OA |
| OB |
| OC |
点评：本题考查了向量的平行四边形法则与三角形法则，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
过椭圆
+
=1上一点M（0，2）作圆x2+y2=2的两条切线，点A，B为切点，O为坐标原点，则△AOB的面积为（ ）
| x2 |
| 9 |
| y2 |
| 4 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
设α∈（0，π），且tanα=
，则cosα=（ ）
| 5 |
| A、2 | ||||
B、-
| ||||
C、
| ||||
D、
|