题目内容
(文做)设
<(
)b<(
)a<1,那么( )
| 1 |
| 2015 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| A、aa<bb<ba |
| B、aa<bb<a |
| C、ab<ba<aa |
| D、ab<aa<ba |
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:根据函数f(x)=(
)x为减函数,结合已知可得:0<a<b<1,进而根据函数g(x)=ax为减函数,函数h(x)=xa为增函数,可得答案.
| 1 |
| 2015 |
解答:
解:∵函数f(x)=(
)x为减函数,且
<(
)b<(
)a<1,
∴0<a<b<1,
∴函数g(x)=ax为减函数,即ab<aa,
函数h(x)=xa为增函数,即aa<ba,
故ab<aa<ba,
故选:D
| 1 |
| 2015 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| 1 |
| 2015 |
∴0<a<b<1,
∴函数g(x)=ax为减函数,即ab<aa,
函数h(x)=xa为增函数,即aa<ba,
故ab<aa<ba,
故选:D
点评:本题考查的知识点是指数函数的图象与性质,幂函数的图象与性质,熟练掌握指数函数和幂函数的单调性是解答的关键.

练习册系列答案
相关题目
若圆的一条直径的两个端点分别是(-1,3)和(5,-5),则此圆的方程是( )
| A、x2+y2+4x+2y-20=0 |
| B、x2+y2-4x-2y-20=0 |
| C、x2+y2-4x+2y+20=0 |
| D、x2+y2-4x+2y-20=0 |
已知x0是函数f(x)=ex+
的一个零点,若x1∈(1,x0),x2∈(x0,+∞),则( )
| 1 |
| 1-x |
| A、f(x1)<0,f(x2)>0 |
| B、f(x1)<0,f(x2)<0 |
| C、f(x1)>0,f(x2)<0 |
| D、f(x1)>0,f(x2)>0 |
在△ABC中,a,b,c分别为A,B,C的对边,若sinA、sinB、sinC依次成等比数列,则角B的取值范围是( )
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
已知集合A={y|y=2x,x∈R},B={x||x|≤2,x∈Z},则A∩B=( )
| A、(0,2] |
| B、[0,2] |
| C、{1,2} |
| D、{0,1,2} |
三个函数:y=cosx、y=sinx、y=tanx,从中随机抽出一个函数,则抽出的函数式偶函数的概率为( )
A、
| ||
| B、0 | ||
C、
| ||
| D、1 |
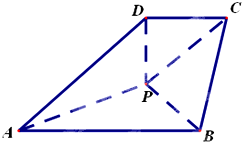 四棱锥P-ABCD如图放置,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.
四棱锥P-ABCD如图放置,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.