题目内容
已知函数f(x)=x3-3x,g(x)=ex-ax(a∈R).其中e是自然对数的底数.
(Ⅰ)求曲线f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若函数F(x)=g(x)-1-xlnx(x∈(0,2]),求证:当a<e-1时,函数F(x)无零点;
(Ⅲ)已知正数m满足:存在x0∈[1,+∞)使得g(x0)+g(-x0)<mf(-x0)成立,且me-1>em-1,
求m的取值范围.
(Ⅰ)求曲线f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若函数F(x)=g(x)-1-xlnx(x∈(0,2]),求证:当a<e-1时,函数F(x)无零点;
(Ⅲ)已知正数m满足:存在x0∈[1,+∞)使得g(x0)+g(-x0)<mf(-x0)成立,且me-1>em-1,
求m的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:计算题,证明题,函数的性质及应用,导数的概念及应用,导数的综合应用
分析:(Ⅰ)求导f′(x)=3x2-3,从而得到切线斜率为f′(2)=9,从而写出切线方程;
(Ⅱ)化简F(x)=ex-1-ax-xlnx,从而得a=
-lnx,设h(x)=
-lnx,求导h′(x)=
,从而化为最值问题;
(Ⅲ)化简G(x)=g(x)+g(-x)=ex+e-x,从而G′(x)=ex-e-x,当x>1时G′(x)>0,从而证明单调性;再令h(x)=mf(-x)=m(-x3+3x),h′(x)=-3m(x2-1),从而确定函数的单调性;从而可化得(e-1)lnm-m+1>0,设H(m)=(e-1)lnm-m+1,从而求导H′(m)=
-1=
, m>0,化为最值问题.
(Ⅱ)化简F(x)=ex-1-ax-xlnx,从而得a=
| ex-1 |
| x |
| ex-1 |
| x |
| (ex-1)(x-1) |
| x2 |
(Ⅲ)化简G(x)=g(x)+g(-x)=ex+e-x,从而G′(x)=ex-e-x,当x>1时G′(x)>0,从而证明单调性;再令h(x)=mf(-x)=m(-x3+3x),h′(x)=-3m(x2-1),从而确定函数的单调性;从而可化得(e-1)lnm-m+1>0,设H(m)=(e-1)lnm-m+1,从而求导H′(m)=
| e-1 |
| m |
| e-1-m |
| m |
解答:
解:(Ⅰ)由f(x)=x3-3x得f′(x)=3x2-3,
因点(2,f(2))在曲线上,
所以切线斜率为f′(2)=9,
切线方程为y-2=9(x-2),
故直线方程为9x-y-16=0;
(Ⅱ)证明:因为F(x)=ex-1-ax-xlnx,
由F(x)=0得,a=
-lnx,
设h(x)=
-lnx,
则h′(x)=
,
当0<x<1时,h′(x)<0,当1<x<2时,h′(x)>0,
所以h(x)在(0,1)单调递减,(1,2)单调递增,
又h(1)=e-1,
所以当a<e-1时,函数F(x)无零点;
(Ⅲ)G(x)=g(x)+g(-x)=ex+e-x,
则G′(x)=ex-e-x,当x>1时G′(x)>0,
∴G(x)在(1,+∞)上单调递增,
令h(x)=mf(-x)=m(-x3+3x),h′(x)=-3m(x2-1),
∵m>0,x>1,
∴h′(x)<0,
即h(x)在x∈(1,+∞)上单调递减,
∵存在x0∈[1,+∞),使得g(x0)+g(-x0)<m(-x03+3x0),
∴G(1)=e+
<2m,
即m>
(e+
),
∵me-1>em-1,
∴(e-1)lnm>m-1,
即(e-1)lnm-m+1>0,
设H(m)=(e-1)lnm-m+1,
则H′(m)=
-1=
, m>0,
当0<m<e-1时,H′(m)>0,H(m)单调递增,
当m>e-1时,H′(m)<0,H(m)单调递减,
而H(1)=H(e)=0,
所以使H(m)>0的m满足1<m<e;
故符合条件的m满足
(e+
)<m<e.
因点(2,f(2))在曲线上,
所以切线斜率为f′(2)=9,
切线方程为y-2=9(x-2),
故直线方程为9x-y-16=0;
(Ⅱ)证明:因为F(x)=ex-1-ax-xlnx,
由F(x)=0得,a=
| ex-1 |
| x |
设h(x)=
| ex-1 |
| x |
则h′(x)=
| (ex-1)(x-1) |
| x2 |
当0<x<1时,h′(x)<0,当1<x<2时,h′(x)>0,
所以h(x)在(0,1)单调递减,(1,2)单调递增,
又h(1)=e-1,
所以当a<e-1时,函数F(x)无零点;
(Ⅲ)G(x)=g(x)+g(-x)=ex+e-x,
则G′(x)=ex-e-x,当x>1时G′(x)>0,
∴G(x)在(1,+∞)上单调递增,
令h(x)=mf(-x)=m(-x3+3x),h′(x)=-3m(x2-1),
∵m>0,x>1,
∴h′(x)<0,
即h(x)在x∈(1,+∞)上单调递减,
∵存在x0∈[1,+∞),使得g(x0)+g(-x0)<m(-x03+3x0),
∴G(1)=e+
| 1 |
| e |
即m>
| 1 |
| 2 |
| 1 |
| e |
∵me-1>em-1,
∴(e-1)lnm>m-1,
即(e-1)lnm-m+1>0,
设H(m)=(e-1)lnm-m+1,
则H′(m)=
| e-1 |
| m |
| e-1-m |
| m |
当0<m<e-1时,H′(m)>0,H(m)单调递增,
当m>e-1时,H′(m)<0,H(m)单调递减,
而H(1)=H(e)=0,
所以使H(m)>0的m满足1<m<e;
故符合条件的m满足
| 1 |
| 2 |
| 1 |
| e |
点评:本题考查了导数的综合应用及恒成立问题化为最值问题的应用,属于难题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
某单位200名职工中,年龄在50岁以上占20%,40~50岁占30%,40岁以下占50%;现要从中抽取40名职工作样本.若用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号,6~10号,…,196~200号).若第5组抽出的号码为22,则第8组抽出的号码应是①;若用分层抽样方法,则40岁以下年龄段应抽取②人.①②两处应填写的数据分别为( )
| A、82,20 | B、37,20 |
| C、37,4 | D、37,50 |
在平面直角坐标系xOy中,如果菱形OABC的边长为2,点B在y轴上,则菱形内(不含边界)的整点(横纵坐标都是整数的点)个数的取值集合是( )
| A、{1,3} |
| B、{0,1,3} |
| C、{0,1,3,4} |
| D、{0,1,2,3,4} |
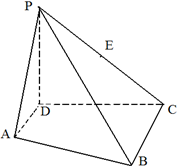 如图,已知PD⊥平面ABCD,AD⊥CD,AD∥BC,PD=DC=BC;
如图,已知PD⊥平面ABCD,AD⊥CD,AD∥BC,PD=DC=BC; 如图,某三棱柱的正视图中的实线部分是边长为4的正方形,俯视图是等边三角形,则该三棱柱的侧视图的面积为
如图,某三棱柱的正视图中的实线部分是边长为4的正方形,俯视图是等边三角形,则该三棱柱的侧视图的面积为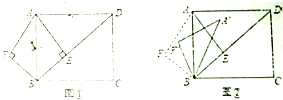 已知:如图①,在矩形ABCD中,AB=5,AD=
已知:如图①,在矩形ABCD中,AB=5,AD=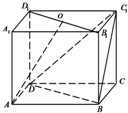 如图.正方体ABCD-A1B1C1D1中,点O为B1D1的中点.求证:
如图.正方体ABCD-A1B1C1D1中,点O为B1D1的中点.求证: