题目内容
在平面直角坐标系xOy中,如果菱形OABC的边长为2,点B在y轴上,则菱形内(不含边界)的整点(横纵坐标都是整数的点)个数的取值集合是( )
| A、{1,3} |
| B、{0,1,3} |
| C、{0,1,3,4} |
| D、{0,1,2,3,4} |
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:根据菱形的不同位置进行判断即可.
解答:
解:根据对称性我们只研究在x轴上方的整点情况,∵菱形OABC的边长为2,点B在y轴上,
∴A,C点在半径为2的圆上,且A,C关于y轴对称,
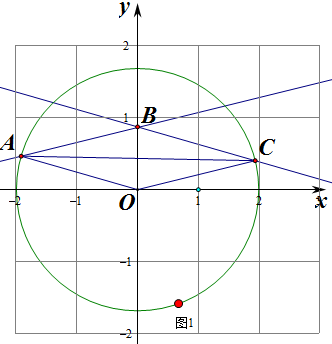
①如图1,若对角线OB的长度OB≤1,此时区域内整点个数为0,排除A,
②如图2.此时区域内整点为(0,1),个数为1,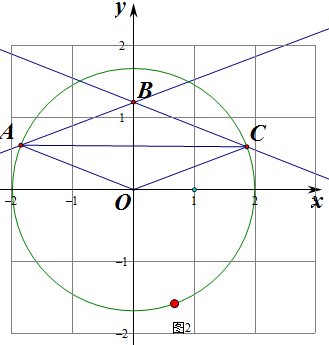
③如图3,此时区域内整点为(-1,1),(0,1),(1,1),个数为3,
④如图4.则此时区域内整点为(-1,1),(0,1),(0,2),(1,1),个数为4个,
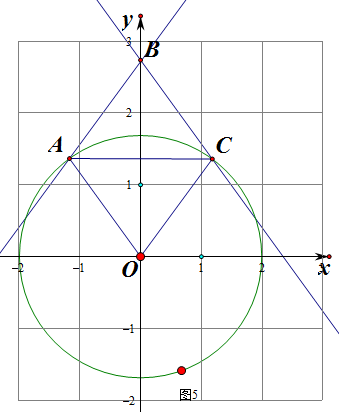
⑤如图5.则此时区域内整点为(0,1),(0,2),个数为2个,
综上菱形内(不含边界)整点(横纵坐标都是整数的点)个数的取值集合是{0,1,2,3,4},
故选:D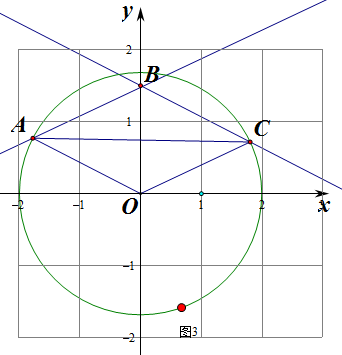
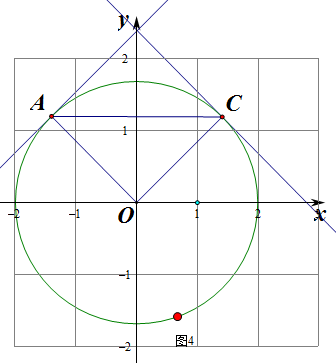
∴A,C点在半径为2的圆上,且A,C关于y轴对称,

①如图1,若对角线OB的长度OB≤1,此时区域内整点个数为0,排除A,
②如图2.此时区域内整点为(0,1),个数为1,

③如图3,此时区域内整点为(-1,1),(0,1),(1,1),个数为3,
④如图4.则此时区域内整点为(-1,1),(0,1),(0,2),(1,1),个数为4个,
⑤如图5.则此时区域内整点为(0,1),(0,2),个数为2个,
综上菱形内(不含边界)整点(横纵坐标都是整数的点)个数的取值集合是{0,1,2,3,4},
故选:D



点评:本题主要考查平面区域内整点的判断,利用数形结合是解决本题的关键.比较复杂.

练习册系列答案
相关题目
设f:x→ln|x|是集合M到集合N的映射,若N={0,1},则M不可能是( )
| A、{1,e} |
| B、{-1,1,e} |
| C、{1,-e,e} |
| D、{0,1,e} |
已知集合A={y|y=
(x≠0)},B={x|x2-x-2≤0},则( )
| |x| |
| x |
| A、A?B | B、B?A |
| C、A=B | D、A∩B=∅ |
已知圆O:x2+y2=2,直线l:x+2y-4=0,点P(x0,y0)在直线l上.若存在圆C上的点Q,使得∠OPQ=45°(O为坐标原点),则x0的取值范围是( )
| A、[0,1] | ||||
B、[0,
| ||||
C、[-
| ||||
D、[-
|
椭圆
+
=1的离心率为( )
| x2 |
| 4 |
| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|