题目内容
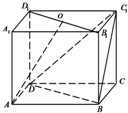 如图.正方体ABCD-A1B1C1D1中,点O为B1D1的中点.求证:
如图.正方体ABCD-A1B1C1D1中,点O为B1D1的中点.求证:(Ⅰ)AO∥面BC1D;
(Ⅱ)AO⊥BD.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)连接AC与BD交于G点,连接OC1,GC1,由OC1∥AG,OC1=AG,可得OA∥GC1,从而可证OA∥平面C1BD.
(Ⅱ)连接OO1,∵正方体ABCD-A1B1C1D1中,点O为B1D1的中点,得到OO1⊥平面ABCD,由线面垂直的性质得到OO1⊥BD,结合AC⊥BD,可得BD⊥平面AOO1,再由线面垂直的性质可证.
(Ⅱ)连接OO1,∵正方体ABCD-A1B1C1D1中,点O为B1D1的中点,得到OO1⊥平面ABCD,由线面垂直的性质得到OO1⊥BD,结合AC⊥BD,可得BD⊥平面AOO1,再由线面垂直的性质可证.
解答:
证明:(Ⅰ)连接AC,BD交于G点,连接OC1,GC1,
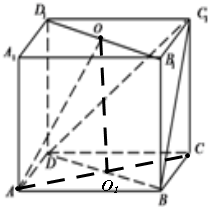
∴在正方体ABCD-A1B1C1D1中,OC1∥AG,OC1=AG,
∴四边形OC1AG为平行四边形,
∴OA∥GC1,
又GC1?平面C1BD,OA?平面C1BD,
∴OA∥平面C1BD.
(Ⅱ)连接OO1,∵正方体ABCD-A1B1C1D1中,点O为B1D1的中点,
∴OO1⊥平面ABCD,
∴OO1⊥BD,
又∵AC⊥BD,
∴BD⊥平面AOO1
∴AO⊥BD.

∴在正方体ABCD-A1B1C1D1中,OC1∥AG,OC1=AG,
∴四边形OC1AG为平行四边形,
∴OA∥GC1,
又GC1?平面C1BD,OA?平面C1BD,
∴OA∥平面C1BD.
(Ⅱ)连接OO1,∵正方体ABCD-A1B1C1D1中,点O为B1D1的中点,
∴OO1⊥平面ABCD,
∴OO1⊥BD,
又∵AC⊥BD,
∴BD⊥平面AOO1
∴AO⊥BD.
点评:本题考查了正方体性质的运用以及线面平行、线面垂直的判定定理和性质定理的运用,考查了学生的空间想象能力,属于基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知全集U={1,2,3,4,5},A={1,2},B={2,3},则(CuA)∩B=( )
| A、{3} |
| B、{1,2,3} |
| C、{5} |
| D、{1,2,3,4,5} |
运行如图所示的程序框图,则输出的结果S为( )


| A、2014 | B、2013 |
| C、1008 | D、1007 |
椭圆
+
=1的离心率为( )
| x2 |
| 4 |
| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|