��Ŀ����
��֪������C��y2=2px��p��0���Ľ���ΪF��AΪC������ԭ�������һ�㣬����A��ֱ��l��C����һ��B����x����������ڵ�D������حFAح=حFDح������A�ĺ�����Ϊ3ʱ����ADFΪ�������Σ�
������C�ķ��̣�
������ֱ��l1��l����l1��C����ֻ��һ��������E��
������֤��ֱ��AE�����㣬������������ꣻ
��������ABE������Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɣ�
������C�ķ��̣�
������ֱ��l1��l����l1��C����ֻ��һ��������E��
������֤��ֱ��AE�����㣬������������ꣻ
��������ABE������Ƿ������Сֵ�������ڣ��������Сֵ���������ڣ���˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����,�����ߵı�����
ר�⣺Բ���ߵĶ��塢�����뷽��,Բ�����е���ֵ�뷶Χ����
��������1�����������ߵĽ��뾶��ʽ����ϵȱ������ε����ʣ������pֵ��
��2�������������A�����꣬���ֱ��AB�ķ��̣�����ֱ��l1��l����l1��C����ֻ��һ��������E�������E�����꣬д��ֱ��AE�ķ��̣������̻�Ϊ��бʽ����������㣻
������ �����ҳ���ʽ�����AB�ij��ȣ������E��ֱ��AB�ľ��룬�õ���������ĺ�����ϵʽ�������û�������ʽ����Сֵ��
��2�������������A�����꣬���ֱ��AB�ķ��̣�����ֱ��l1��l����l1��C����ֻ��һ��������E�������E�����꣬д��ֱ��AE�ķ��̣������̻�Ϊ��бʽ����������㣻
������ �����ҳ���ʽ�����AB�ij��ȣ������E��ֱ��AB�ľ��룬�õ���������ĺ�����ϵʽ�������û�������ʽ����Сֵ��
���
 �⣺��1������A�ĺ�����Ϊ3ʱ������A��AG��x����G��
�⣺��1������A�ĺ�����Ϊ3ʱ������A��AG��x����G��
A��3��
����F��
��0����|AF|=3+
��
��|FD|=|AF|=3+
��
�ߡ�ADFΪ�������Σ�
��|FG|=
|FD|=
+
��
�֡�|FG|=|OG|-|OF|=3-
��
��3-
=
+
��
��p=2��
��C�ķ���Ϊy2=4x��
��D�ڽ���F�����ʱ��|FD|=|AF|=3+
��
��|FD|=2|FG|=2��
-3��=p-6��
�ߡ�ADFΪ�������Σ�
��3+
=p-6�����p=18��
��C�ķ���Ϊy2=36x����ʱ��D��x�Ḻ���ᣬ���������ᣮ
��C�ķ���Ϊy2=4x��
��2����������A��x1��y1����|FD|=|AF|=x1+1��
��D��x1+2��0����
��kAB=-
��
��ֱ��l1��l����ֱ��l1����Ϊy=-
x+m��
��������
����ȥx��y1y2+8y-8m=0 ��
��l1��C����ֻ��һ��������á�=64+32y1m=0����y1m=-2��
��ʱ���̢ٵĽ�Ϊy=-
=2m������y=-
x+m��x=m2����E��m2��2m����
��A������ɻ�Ϊ(
��-
)��ֱ��AE����Ϊy-2m=
��x-m2����
��y-2m=
(x-m2)��
��y=
x-
+2m��
��y=
x-
��
��y=
(x-1)��
��ֱ��AE�����㣨1��0����
������ֱ��AB�ķ���Ϊy-y1=-
(x-
)����x=-
y+
+2��
��������
����ȥx��y2+
y-(
+8)=0��
��y1+y2=-
��
��|AB|=
|y1-y2|=
|2y1+
|��
�ɣ�������E������ΪE(
��-
)����E��ֱ��AB�ľ���Ϊ��
d=
=
��
���ABE�����S=
|AB|•d=
|2y1+
|•|
+
+2|=2|
+
|3��2��23��16��
���ҽ���y1=��2ʱ�Ⱥų�����
���ABE�������СֵΪ16��
 �⣺��1������A�ĺ�����Ϊ3ʱ������A��AG��x����G��
�⣺��1������A�ĺ�����Ϊ3ʱ������A��AG��x����G��A��3��
| 6p |
| p |
| 2 |
| p |
| 2 |
��|FD|=|AF|=3+
| p |
| 2 |
�ߡ�ADFΪ�������Σ�
��|FG|=
| 1 |
| 2 |
| 3 |
| 2 |
| p |
| 4 |
�֡�|FG|=|OG|-|OF|=3-
| p |
| 2 |
��3-
| p |
| 2 |
| 3 |
| 2 |
| p |
| 4 |
��p=2��
��C�ķ���Ϊy2=4x��
��D�ڽ���F�����ʱ��|FD|=|AF|=3+
| p |
| 2 |
��|FD|=2|FG|=2��
| P |
| 2 |
�ߡ�ADFΪ�������Σ�
��3+
| p |
| 2 |
��C�ķ���Ϊy2=36x����ʱ��D��x�Ḻ���ᣬ���������ᣮ
��C�ķ���Ϊy2=4x��
��2����������A��x1��y1����|FD|=|AF|=x1+1��
��D��x1+2��0����
��kAB=-
| y1 |
| 2 |
��ֱ��l1��l����ֱ��l1����Ϊy=-
| y1 |
| 2 |
��������
|
��l1��C����ֻ��һ��������á�=64+32y1m=0����y1m=-2��
��ʱ���̢ٵĽ�Ϊy=-
| 4 |
| y1 |
| y1 |
| 2 |
��A������ɻ�Ϊ(
| 1 |
| m2 |
| 2 |
| m |
2m+
| ||
m2-
|
��y-2m=
| 2m |
| m2-1 |
��y=
| 2m |
| m2-1 |
| 2m3 |
| m2-1 |
��y=
| 2m |
| m2-1 |
| 2m |
| m2-1 |
��y=
| 2m |
| m2-1 |
��ֱ��AE�����㣨1��0����
������ֱ��AB�ķ���Ϊy-y1=-
| y1 |
| 2 |
| ||
| 4 |
| 2 |
| y1 |
| ||
| 4 |
��������
|
| 8 |
| y1 |
| y | 2 1 |
��y1+y2=-
| 8 |
| y1 |
��|AB|=
1+
|
1+
|
| 8 |
| y1 |
�ɣ�������E������ΪE(
| 4 | ||
|
| 4 |
| y1 |
d=
|
| ||||||||||||
|
|
| ||||||||
|
���ABE�����S=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| y1 |
| 4 | ||
|
| ||
| 4 |
| y1 |
| 2 |
| 2 |
| y1 |
���ҽ���y1=��2ʱ�Ⱥų�����
���ABE�������СֵΪ16��
���������⿼���������ߵĶ����Ӧ�á������������߷��̵���������������ֵ���⣮

��ϰ��ϵ�д�
 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
�����Ŀ
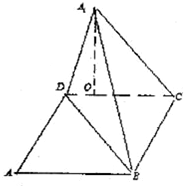 ��ͼ������ABCD�У�AB=10��BC=6���ضԽ���BD�ɡ�ABD����A1BD��λ�ã�ʹA1��ƽ��BCD�ϵ���ӰOǡ����CD�ϣ�
��ͼ������ABCD�У�AB=10��BC=6���ضԽ���BD�ɡ�ABD����A1BD��λ�ã�ʹA1��ƽ��BCD�ϵ���ӰOǡ����CD�ϣ�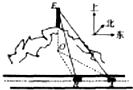 ��ͼ��һ��������һ��ˮƽ�Ĺ�·��������������ʻ����A���ֱ���ɽ��������������E������Ϊ�Ⱥ�ɽ�ŵ�O����O�ǵ�E�ڹ�·����ƽ���ϵ���Ӱ���ķ�λ������ƫ���գ�����ʻakm����B�������ɽ�ŵ�O�ķ�λ������ƫ���£������һ���������ò��������ݺ��йع�ʽд������OE�IJ��裮
��ͼ��һ��������һ��ˮƽ�Ĺ�·��������������ʻ����A���ֱ���ɽ��������������E������Ϊ�Ⱥ�ɽ�ŵ�O����O�ǵ�E�ڹ�·����ƽ���ϵ���Ӱ���ķ�λ������ƫ���գ�����ʻakm����B�������ɽ�ŵ�O�ķ�λ������ƫ���£������һ���������ò��������ݺ��йع�ʽд������OE�IJ��裮 ��ͼ��������AMDE�ı߳�Ϊ2��B��C�ֱ�ΪAM��MD���е㣬������P-ABCDE�У�FΪ��PE���е㣬ƽ��ABF����PD��PC�ֱ��ڵ�G��H��
��ͼ��������AMDE�ı߳�Ϊ2��B��C�ֱ�ΪAM��MD���е㣬������P-ABCDE�У�FΪ��PE���е㣬ƽ��ABF����PD��PC�ֱ��ڵ�G��H��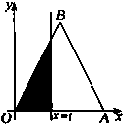 ��ͼ����OAB�DZ߳�Ϊ2���������Σ��ǡ�OABλ��ֱ��x=t��0��t��2������ͼ�ε����Ϊf��t������
��ͼ����OAB�DZ߳�Ϊ2���������Σ��ǡ�OABλ��ֱ��x=t��0��t��2������ͼ�ε����Ϊf��t������