题目内容
设A(-m,0),B(m,0)(m≠0),直线AC,BC相交于C,而且他们的斜率之积为-
,若点P(1,
)是点C的轨迹上的点,直线l的方程为x=2.
(Ⅰ)求点C的轨迹方程;
(Ⅱ)过点E(1,0)的直线与点C的轨迹相交于D,M两点(不经过P点),直线DM与直线l相交于N,记直线PD,PM,PN的斜率分别为k1,k2,k3.求证:k1+k2=2k3.
| 1 |
| m2 |
| ||
| 2 |
(Ⅰ)求点C的轨迹方程;
(Ⅱ)过点E(1,0)的直线与点C的轨迹相交于D,M两点(不经过P点),直线DM与直线l相交于N,记直线PD,PM,PN的斜率分别为k1,k2,k3.求证:k1+k2=2k3.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设点C(x,y)则kAC•kBC=-
,化简后代入点P(1,
),求出m,即可求点C的轨迹方程;
(Ⅱ)假设存在实数μ使得k1+k2=μk3,设D(x1,y1),M(x2,y2),直线DM的方程为y=k(x-1)代入点C的轨迹方程,利用韦达定理求出两根和与两根之积,表示出直线PD,PM,PN的斜率分别为k1,k2,k3.通过三点共线即可求出μ,得到所证明的k1+k2=2k3.
| 1 |
| m2 |
| ||
| 2 |
(Ⅱ)假设存在实数μ使得k1+k2=μk3,设D(x1,y1),M(x2,y2),直线DM的方程为y=k(x-1)代入点C的轨迹方程,利用韦达定理求出两根和与两根之积,表示出直线PD,PM,PN的斜率分别为k1,k2,k3.通过三点共线即可求出μ,得到所证明的k1+k2=2k3.
解答:
解:(Ⅰ)设点C(x,y)则kAC•kBC=
•
=-
(x≠±m)--(2分)
化简得
+y2=1(x≠±m)----------------------------------(3分)
∵P(1,
)在点C的轨迹上,∴
+
=1------------(4分)
∴m2=2,∴点C的轨迹方程为:
+y2=1(x≠±
)------------(6分)
(Ⅱ)假设存在实数μ使得k1+k2=μk3,
由题意设直线DM的方程为y=k(x-1)代入点C的轨迹方程
+y2=1(x≠±
)
得(1+2k2)x2-4k2x+2(k2-1)=0---------------------------(8分)
设D(x1,y1),M(x2,y2),
∴x1+x2=
,x1•x2=
---------(9分)
根据题意得N(2,k),从而k1=
,k2=
,k3=
=k-
.
又因为E、D、M三点共线,∴k=
=
-------------------(10分)
∴k1+k2=
+
=
+
-
(
+
)
=2k-
•
=2k-
•
=2k-
=2k3-(12分)
故存在实数μ=2符合题意-----------------------(13分)
故k1+k2=2k3--------------------(13分)(文科)
| y |
| x+m |
| y |
| x-m |
| 1 |
| m2 |
化简得
| x2 |
| m2 |
∵P(1,
| ||
| 2 |
| 1 |
| m2 |
| 1 |
| 2 |
∴m2=2,∴点C的轨迹方程为:
| x2 |
| 2 |
| 2 |
(Ⅱ)假设存在实数μ使得k1+k2=μk3,
由题意设直线DM的方程为y=k(x-1)代入点C的轨迹方程
| x2 |
| 2 |
| 2 |
得(1+2k2)x2-4k2x+2(k2-1)=0---------------------------(8分)
设D(x1,y1),M(x2,y2),
∴x1+x2=
| 4k2 |
| 1+2k2 |
| 2(k2-1) |
| 1+2k2 |
根据题意得N(2,k),从而k1=
y1-
| ||||
| x1-1 |
y2-
| ||||
| x2-1 |
k-
| ||||
| 2-1 |
| ||
| 2 |
又因为E、D、M三点共线,∴k=
| y1 |
| x1-1 |
| y2 |
| x2-1 |
∴k1+k2=
y1-
| ||||
| x1-1 |
y2-
| ||||
| x2-1 |
| y1 |
| x1-1 |
| y2 |
| x2-1 |
| ||
| 2 |
| 1 |
| x1-1 |
| 1 |
| x2-1 |
=2k-
| ||
| 2 |
| x1+x2-2 |
| x1x2-(x1+x2)+1 |
| ||
| 2 |
| ||||
|
| 2 |
故存在实数μ=2符合题意-----------------------(13分)
故k1+k2=2k3--------------------(13分)(文科)
点评:本题考查直线与圆锥曲线的位置关系,轨迹方程的求法,考查分析问题与解答问题的能力,计算量大,难度高.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
若复数z满足:(3-i)z=3+i(i为虚数单位),则复数z在复平面内对应的点所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
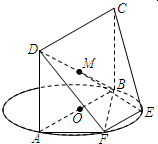 如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=
如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=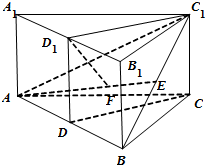 如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.
如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.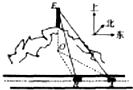 如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.
如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.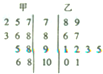 某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.