题目内容
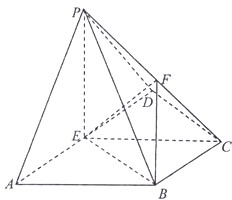 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.(1)求证:AP∥平面EFB;
(2)若△PAD是等边三角形,求直线EF与平面PAD所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)要证AP∥平面EFB,可通过线面平行的判定定理来证明;
(2)要求直线EF与平面PAD所成角的正弦值,须找到线面角,再由边角关系即可求出.
(2)要求直线EF与平面PAD所成角的正弦值,须找到线面角,再由边角关系即可求出.
解答:
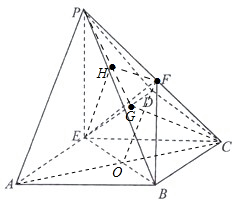 解:(1)证:连AC交EB与O,连OF
解:(1)证:连AC交EB与O,连OF
由ABCE为平行四边形∴O为AC中点
在△APC中,OF∥AP
又∵OF?平面EFB,AP?平面EFB
∴AP∥平面EFB
(2)过C作CG⊥AD于G,连PG
由侧面PAD⊥底面ABCD知CG⊥平面PAD,
取PG中点H,连接HF、EH,则HF⊥平面PAD
∴∠FEH即为所求线面角
由AB=1,得HF=
CG=
,EF=
PC=1,
在Rt△FEH中sin∠FEH=
∴所求的角的正弦值为
.
 解:(1)证:连AC交EB与O,连OF
解:(1)证:连AC交EB与O,连OF 由ABCE为平行四边形∴O为AC中点
在△APC中,OF∥AP
又∵OF?平面EFB,AP?平面EFB
∴AP∥平面EFB
(2)过C作CG⊥AD于G,连PG
由侧面PAD⊥底面ABCD知CG⊥平面PAD,
取PG中点H,连接HF、EH,则HF⊥平面PAD
∴∠FEH即为所求线面角
由AB=1,得HF=
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
在Rt△FEH中sin∠FEH=
| ||
| 4 |
| ||
| 4 |
点评:本题考查线面平行、线面垂直以及线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
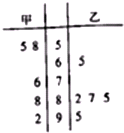 如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为
如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
过抛物线y2=2px(p>0)的焦点作倾斜角为30°的直线l与抛物线交于P、Q两点,分别过P、Q两点作PP1,QQ1垂直于抛物线的准线于P1、Q1,若|PQ|=2,则四边形PP1Q1Q的面积是( )
A、
| ||
| B、2 | ||
| C、3 | ||
| D、1 |
已知边长为1的正三角形ABC,D是BC的中点,E是AC上一点且AE=2EC.则
•
=( )
| AD |
| BE |
A、
| ||
B、-
| ||
| C、0 | ||
| D、4 |
若复数z满足:(3-i)z=3+i(i为虚数单位),则复数z在复平面内对应的点所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
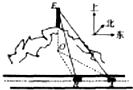 如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.
如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.