题目内容
17.下列说法正确的是( )| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}$<1“是“a>1“的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题 |
分析 判断原命题逆否命题的真假,可判断A;根据充要条件的定义,可判断B;写出原命题的否定,可判断C;写出原命题的逆命题,可判断D.
解答 解:?x,y∈R,若x+y≠0,则x≠1且y≠-1的逆否命题为:?x,y∈R,若x=1或y=-1,则x+y=0,为假命题,故A错误;
a∈R,“$\frac{1}{a}$<1”?“a<0,或a>1”是“a>1”的必要不充分条件,故B正确;
命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3≥0”,故C错误;
“若am2<bm2,则a<b”的逆命题为“若a<b,则am2<bm2”为假命题,故D错误;,
故选:B
点评 本题以命题的真假判断与应用为载体,考查四种命题,命题的否定,不等式的基本性质,充要条件等知识点,难度中档.

练习册系列答案
相关题目
12.已知集合A={x|0<x≤3,x∈N},B={x|y=$\sqrt{{x}^{2}-1}$},则集合A∩B为( )
| A. | {1,2} | B. | {1,2,3} | C. | {0,1,2} | D. | {0,1,2,3} |
2.在△ABC中,A、B、C的对边分别为a、b、c,若B=$\frac{π}{3}$,b=6,sinA-2sinC=0,则a=( )
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 12 |
9.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≥3}\\{f(x+1),x<3}\end{array}\right.$f(log23)的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
6.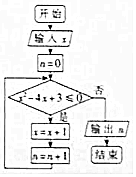 执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )
执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )
 执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )
执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
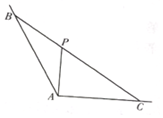 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.