题目内容
12.已知集合A={x|0<x≤3,x∈N},B={x|y=$\sqrt{{x}^{2}-1}$},则集合A∩B为( )| A. | {1,2} | B. | {1,2,3} | C. | {0,1,2} | D. | {0,1,2,3} |
分析 分别求出集合A和B,由此利用交集定义能求出集合A∩B.
解答 解:∵集合A={x|0<x≤3,x∈N}={1,2,3},
B={x|y=$\sqrt{{x}^{2}-1}$}={x|x≥1或x≤-1},
∴集合A∩B={1,2,3}.
故选:B.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
相关题目
2.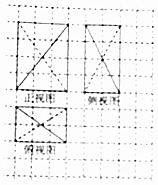 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )| A. | 24π | B. | 29π | C. | 48π | D. | 58π |
20.已知实数x,y满足$\left\{\begin{array}{l}{y≥x+2}\\{x+y≤6}\\{x≥1}\end{array}\right.$,则z=2|x-2|+|y|的最小值是( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
17.下列说法正确的是( )
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}$<1“是“a>1“的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题 |
4.在△ABC中,AC=2AB=2,∠BAC=120°,O是BC的中点,M是AO上一点,且$\overrightarrow{AO}$=3$\overrightarrow{MO}$,则$\overrightarrow{MB}$$•\overrightarrow{MC}$的值是( )
| A. | -$\frac{5}{3}$ | B. | -$\frac{7}{6}$ | C. | -$\frac{7}{3}$ | D. | -$\frac{5}{6}$ |
1.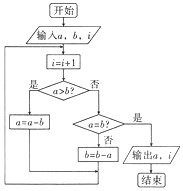 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )| A. | 2,5 | B. | 2,4 | C. | 0,4 | D. | 0,5 |
16.已知实数x,y满足$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{0≤y≤k}\end{array}\right.$,且z=x+y的最大值为6,则(x+5)2+y2的最小值为( )
| A. | 5 | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |