题目内容
7.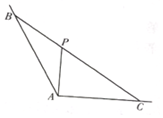 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.(Ⅰ)若AB=3,求PC;
(Ⅱ)求$\frac{1}{PB}$$+\frac{1}{PC}$的取值范围.
分析 (Ⅰ)根据余弦定理求出PB的长,再解直角三角形即可求出答案,
(Ⅱ)根据正弦定理得PB=$\frac{AP}{2sin(θ-\frac{π}{6})}$,在Rt△APC中,PC=$\frac{AP}{cosθ}$,继而得到于是$\frac{1}{PB}$+$\frac{1}{PC}$=sinθ,根据正弦函数的图象和性质即可求出答案.
解答 解:(Ⅰ)在△PAB中,由余弦定理知PB2=AP2+AB2-2AP•ABcos$\frac{π}{6}$=3,得PB=$\sqrt{3}$=AP,
则∠BPA=$\frac{2π}{3}$,∠APC=$\frac{π}{3}$,
在Rt△APC中,PC=$\frac{AP}{cos\frac{π}{3}}$=2$\sqrt{3}$,
(Ⅱ)因为∠APC=θ,则∠ABP=θ-$\frac{π}{6}$,
在Rt△APC中,PC=$\frac{AP}{cosθ}$,
在△PAB中,由正弦定理知$\frac{AP}{sin(θ-\frac{π}{6})}$=$\frac{PB}{sin\frac{π}{6}}$,得PB=$\frac{AP}{2sin(θ-\frac{π}{6})}$,
于是$\frac{1}{PB}$+$\frac{1}{PC}$=$\frac{2sin(θ-\frac{π}{6})}{AP}$+$\frac{cosθ}{AP}$=$\frac{\sqrt{3}sinθ}{AP}$=sinθ,
由题意知$\frac{π}{6}$<θ<$\frac{π}{2}$,
故$\frac{1}{2}$<sinθ<1,
即$\frac{1}{PB}$+$\frac{1}{PC}$的取值范围为($\frac{1}{2}$,1)
点评 本题考查了正弦定理和余弦定理以及正弦函数的性质,属于中档题.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
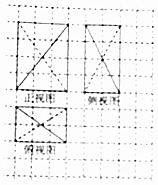 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )| A. | 24π | B. | 29π | C. | 48π | D. | 58π |
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}$<1“是“a>1“的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题 |