题目内容
设f(x)=asin(πx+α)+bcos(πx+β)+4,其中a,b,α,β均为非零的常数,f(1988)=3,则f(2008)的值为( )
| A、1 | B、3 | C、5 | D、不确定 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由条件利用诱导公式求得asinα+bcosβ=-7,再利用诱导公式化简 f(2008)=asinα+bcosβ+4,运算求得结果.
解答:
解:∵f(1998)=asin(1998π+α)+bcos(1998π+β)+4=asinα+bcosβ+4=-3,
∴asinα+bcosβ=-7,
故f(2008)=asin(2008π+α)+bcos(2008π+β)+4=asinα+bcosβ+4=-7+4=3,
故选:B.
∴asinα+bcosβ=-7,
故f(2008)=asin(2008π+α)+bcos(2008π+β)+4=asinα+bcosβ+4=-7+4=3,
故选:B.
点评:本题主要考查利用诱导公式进行化简求值,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
已知命题p:“?x∈R,总有x2-x+1>0”的否定是“?x∈R,使得x2-x+1≤0”;命题q:在△ABC中,“A>
”是“sinA>
”的必要不充分条件.则有( )
| π |
| 4 |
| ||
| 2 |
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
若直线ax+by+1=0(a>0,b>0)过圆x2+y2+2x+2y=0的圆心,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、2 | B、4 | C、8 | D、16 |
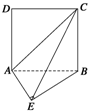 如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )