题目内容
设P是线段P1P2上的一个三等分点,且P1(x1,y1),P2(x2,y2),求点P的坐标.
考点:线段的定比分点
专题:平面向量及应用
分析:
=
或
=
,得出
=(x2-x1,y2-y1),
=(x-x1,y-y1),
=(x2-x,y2-y),解方程求解即可.
| P1P |
| 1 |
| 3 |
| P1P2 |
| PP2 |
| 2 |
| 3 |
| P 1P2 |
| P 1P2 |
| P1P |
| PP2 |
解答:
解:∵设P是线段P1P2上的一个三等分点,P(x,y),
∴
=
,
=
,
∵∵
=(x2-x1,y2-y1),
=(x-x1,y-y1),
=(x2-x,y2-y),
∴
(x2-x1)=x-x1,
(y2-y1)=y-y1,或
(x2-x1)=x2-x,
(y2-y1)=y2-y,
求解:x=
,y=
,或x=
,y=
∴P(
,
),或P(
,
)
∴
| P1P |
| 1 |
| 3 |
| P1P2 |
| PP2 |
| 2 |
| 3 |
| P 1P2 |
∵∵
| P 1P2 |
| P1P |
| PP2 |
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
求解:x=
| x1+2x2 |
| 3 |
| y1+2y2 |
| 3 |
| 2x1+x2 |
| 3 |
| 2y1+y2 |
| 3 |
∴P(
| x1+2x2 |
| 3 |
| y1+2y2 |
| 3 |
| 2x1+x2 |
| 3 |
| 2y1+y2 |
| 3 |
点评:本题考查线段的定比分点,考查学生计算能力,是基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
tan
=( )
| 5π |
| 6 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中( )


| A、AB与CD所成的角为60° |
| B、AB与CD相交 |
| C、AB⊥CD |
| D、AB∥CD |
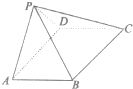 如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.