题目内容

下列函数中，以为π最小正周期的偶函数，且在（0，
π
2
）内递增的是（　　）
A、y=sin|x|
B、y=|sinx|
C、y=|cosx|
D、y=cos|x|
考点：正弦函数的图象,余弦函数的图象
专题：三角函数的图像与性质
分析：分别根据函数的单调性奇偶性和周期性进行判定即可得到结论．
解答： 解：A．y=sin|x|是偶函数，在（0，
π
2
）内递增，但不是周期函数．
B．y=|sinx|是偶函数，在（0，
π
2
）内递增，周期为π，是周期函数．满足条件．
C．y=|cosx|是偶函数，在（0，
π
2
）内递递减，周期为π，是周期函数．．
D．y=cos|x|是偶函数，在（0，
π
2
）内递减，但不是周期函数，
故选：B
点评：本题主要考查三角函数的图象和性质，要求熟练掌握三角函数的周期性，单调性和奇偶性的性质．
练习册系列答案
相关题目
执行如图所示的程序框图，如果输出2，那么判断框内应填入的条件是（　　）
A、k≤3？B、k≤4？
C、k＞3？D、k＞4？
设a＞b＞c，k∈R，且（a-c）•（
1
a-b
+
1
b-c
）≥k恒成立，则k的最大值为（　　）
A、2B、3C、4D、5
复数z=
2
1-i
，则
.
z
=（　　）
A、1+iB、1-i
C、-1+iD、-1-i
用数学归纳法证明1+a+a2+…+an+1=
1-an+2
1-a
（a≠1，n∈N*），在验证当n=1时，等式左边应为（　　）
A、1
B、1+a
C、1+a+a2
D、1+a+a2+a3
在直角坐标系xOy上取两个定点A1（-2，0），A2（2，0），再取两个动点N1（0，m），N2（0，n），且mn=3．
（1）求直线A1N1与A2N2交点的轨迹M的方程；
（2）已知点G（1，0）和G′（-1，0），点P在轨迹M上运动，现以P为圆心，PG为半径作圆P，试探究是否存在一个以点G′（-1，0）为圆心的定圆，总与圆P内切？若存在，求出该定圆的方程；若不存在，请说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，以原点为圆心，椭圆的短半轴长为半径的圆与直线x-y+
2
=0相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过点M（2，0）的直线与椭圆C相交于两点A、B，设P为椭圆上一点，且满足
OA
+
OB
=t
OP
（其中O为坐标原点），求整数t的最大值．
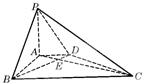如图，在底面为直角梯形的四棱锥P-ABCD中，AD∥BC，∠ABC=90°PA⊥平面，PA=4，AD=2，AB=2
3
，BC=6．
（Ⅰ）求证：BD⊥平面PAC
（Ⅱ）求二面角P-BD-A的大小．
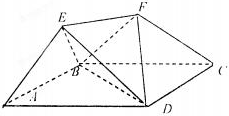如图，底面ABCD是边长为2的菱形，且∠BAD=
π
3
，分别以△ABD与△CBD为底面作相同的正三棱锥E-ABD与F-CBD，且∠AEB=
π
2
．
（1）求证：EF∥平面ABCD；
（2）求多面体ABCDEF的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网