题目内容
已知平面直角坐标系中,点O为原点,A(-3,-4),B(5,-12).
(1)求cos∠AOB和△AOB的面积;
(2)若四边形AEBF为平行四边形,且
=(1,1),求平行四边形AEBF的面积.
(1)求cos∠AOB和△AOB的面积;
(2)若四边形AEBF为平行四边形,且
| EF |
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)由题意可得
和
的坐标,可得|
|=5,|
|=13,根据cos∠AOB=
的值,求得sin∠AOB 的值,从而求得△AOB的面积为
•|
|•|
|•sin∠AOB 的值.
(2)设点E(x,y),则点F(1+x,1+y),根据
=
求得x和y的值.再由
•
=0,可得AE⊥AF,
平行四边形AEBF为正方形,由此求得它的面积.
| OA |
| OB |
| OA |
| OB |
| ||||
|
|
| 1 |
| 2 |
| OA |
| OB |
(2)设点E(x,y),则点F(1+x,1+y),根据
| AE |
| FB |
| AE |
| AF |
平行四边形AEBF为正方形,由此求得它的面积.
解答:
解:(1)由题意可得
=(-3,-4),
=(5,-12),∴|
|=5,|
|=13,
∴cos∠AOB=
=
=
,∴sin∠AOB=
,
△AOB的面积为
•|
|•|
|•sin∠AOB=
.
(2)若四边形AEBF为平行四边形,且
=(1,1),设点E(x,y),则点F(1+x,1+y),
根据
=
可得 (x+3,y+4)=(4-x,-13-y),解得x=
,y=-
.
∴
=(
,-
),
=(
,-
),∴
•
=0,AE⊥AF,
故平行四边形AEBF为正方形,故它的面积为|
|2=
+
=
.
| OA |
| OB |
| OA |
| OB |
∴cos∠AOB=
| ||||
|
|
| -15+48 |
| 5×13 |
| 33 |
| 65 |
| ||
| 65 |
△AOB的面积为
| 1 |
| 2 |
| OA |
| OB |
| ||
| 2 |
(2)若四边形AEBF为平行四边形,且
| EF |
根据
| AE |
| FB |
| 1 |
| 2 |
| 17 |
| 2 |
∴
| AE |
| 7 |
| 2 |
| 9 |
| 2 |
| AF |
| 9 |
| 2 |
| 7 |
| 2 |
| AE |
| AF |
故平行四边形AEBF为正方形,故它的面积为|
. |
| AE |
| 49 |
| 4 |
| 81 |
| 4 |
| 65 |
| 2 |
点评:本题主要考查两个向量的数量积的定义、两个向量的数量积公式、正弦定理和余弦定理的应用,两个向量坐标形式的运算,两个向量垂直的性质,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上任一点.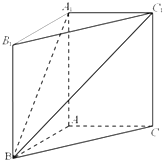 如图,在直三棱柱ABC-A1B1C1中,AC=AB=
如图,在直三棱柱ABC-A1B1C1中,AC=AB=