题目内容
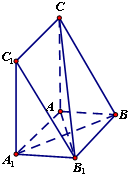 如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.
如图,三棱柱ABC-A1B1C1中,∠CAA1=∠A1AB=∠BAC=90°,AB=AA1=1,AC=2.(1)求证:A1B⊥平面AB1C;
(2)求直线B1C与平面ACC1A1所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明A1B⊥平面AB1C,利用线面垂直的判定,证明A1B垂直于平面AB1C中两条相交直线即可;
(2)连接A1C,证明∠B1CA1是直线B1C与平面ACC1A1所成角,再求直线B1C与平面ACC1A1所成角的正弦值.
(2)连接A1C,证明∠B1CA1是直线B1C与平面ACC1A1所成角,再求直线B1C与平面ACC1A1所成角的正弦值.
解答:
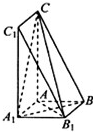 (1)证明:∵∠CAA1=∠BAC=90°,
(1)证明:∵∠CAA1=∠BAC=90°,
∴CA⊥AA1,CA⊥AB,
∵A1A∩AB=A,
∴CA⊥平面A1B1BA,
∵A1B?平面A1B1BA,
∴CA⊥A1B,
∵四边形A1B1BA为正方形,
∴A1B⊥AB1,
∵AC∩AB1=A,
∴A1B⊥平面AB1C;
(2)解:连接A1C,则B1A1⊥AA1,B1A1⊥AC,
∵AA1∩AC=A,
∴B1A1⊥平面ACC1A1,
∴∠B1CA1是直线B1C与平面ACC1A1所成角.
在矩形ACC1A1中,AA1=1,AC=2,∴A1C=
,
∵A1B1=AB=1,
∴在Rt△A1B1C中,CB1=
,
∴sin∠B1CA1=
.
 (1)证明:∵∠CAA1=∠BAC=90°,
(1)证明:∵∠CAA1=∠BAC=90°,∴CA⊥AA1,CA⊥AB,
∵A1A∩AB=A,
∴CA⊥平面A1B1BA,
∵A1B?平面A1B1BA,
∴CA⊥A1B,
∵四边形A1B1BA为正方形,
∴A1B⊥AB1,
∵AC∩AB1=A,
∴A1B⊥平面AB1C;
(2)解:连接A1C,则B1A1⊥AA1,B1A1⊥AC,
∵AA1∩AC=A,
∴B1A1⊥平面ACC1A1,
∴∠B1CA1是直线B1C与平面ACC1A1所成角.
在矩形ACC1A1中,AA1=1,AC=2,∴A1C=
| 5 |
∵A1B1=AB=1,
∴在Rt△A1B1C中,CB1=
| 6 |
∴sin∠B1CA1=
| ||
| 6 |
点评:本题主要考查异面直线所成的角的定义和求法,体现了转化的数学思想,直线和平面垂直的判定定理的应用,属于中档题.

练习册系列答案
相关题目
Sn是数列{an}的前n项和,an=
,则S1=1-
,S2=1-
,S3=1-
,S4=1-
,由此可以归纳出( )
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、Sn=1-
| ||
B、Sn=1-
| ||
C、Sn=1-
| ||
D、Sn=1-
|
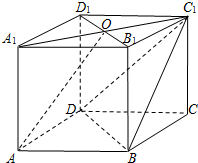 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1